NCERT Solutions Class 7 Mathematics
Chapter – 6 (The Triangle and its Properties)
The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 6 The Triangle and its Properties Exercise 6.4 has been provided here to help the students in solving the questions from this exercise.
Chapter : 6 The Triangles and its Properties
- NCERT Solution Class 7 Maths Exercise – 6.1
- NCERT Solution Class 7 Maths Exercise – 6.2
- NCERT Solution Class 7 Maths Exercise – 6.3
- NCERT Solution Class 7 Maths Exercise – 6.5
Exercise – 6.4
1. Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution –
(i) 2 cm, 3 cm, 5 cm
Sum of the two sides = 2 cm + 3 cm = 5 cm Third side = 5 cm
We have, Sum of any two sides = the third side i.e. 5 cm = 5 cm
Hence, the triangle is not possible.
(ii) 3 cm, 6 cm, 7 cm
Sum of the two sides = 3 cm + 6 cm = 9 cm Third side = 7 cm
We have sum of any two sides > the third
side. i.e. 9 cm > 7 cm
Hence, the triangle is possible.
(iii) 6 cm, 3 cm, 2 cm
Sum of the two sides = 3 cm + 2 cm – 5 cm Third side = 6 cm
We have, sum of any two sides < the third sid6 i.e. 5 cm < 6 cm Hence, the triangle is not possible.
2. Take any point O in the interior of a triangle PQR. Is
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Solution –
If we take any point O in the interior of a triangle PQR and join OR, OP, OQ.
Then, we get three triangles ΔOPQ, ΔOQR and ΔORP is shown in the figure below.
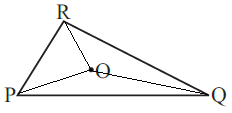
The sum of the length of any two sides is always greater than the third side.
(i) OP + OQ > PQ?
Yes, In ∆OPQ, we have
OP + OQ > PQ
[Sum of any two sides of a triangle is greater than the third side]
(ii) OQ + OR > QR?
Yes, In ∆OQR, we have OQ + OR > QR
[Sum of any two sides of a triangle is greater than the third side]
(iii) OR + OP > RP?
Yes, In ∆OPR, we have OR + OP > RP
[Sum of any two sides of a triangle is greater than the third side]
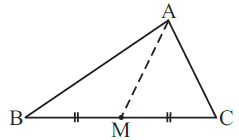
3. AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC.)
Solution –
We know that,
The sum of the length of any two sides is always greater than the third side.
Now consider the ΔABM,
Here, AB + BM > AM ———– [equation (i)]
Then, consider the ΔACM
Here, AC + CM > AM ———– [equation (ii)]
By adding equation (i) and (ii) we get,
AB + BM + AC + CM > AM + AM
From the figure we have, BC = BM + CM
AB + BC + AC > 2 AM
Hence, the given expression is true.
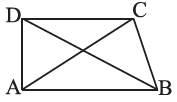
4. ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
Solution –
We know that,
The sum of the length of any two sides is always greater than the third side.
Now consider the ΔABC,
Here, AB + BC > CA ———- [equation (i)]
Then, consider the ΔBCD
Here, BC + CD > DB ———- [equation (ii)]
Consider the ΔCDA
Here, CD + DA > AC ———- [equation (iii)]
Consider the ΔDAB
Here, DA + AB > DB ———- [equation (iv)]
By adding equation (i), (ii), (iii) and (iv) we get,
AB + BC + BC + CD + CD + DA + DA + AB > CA + DB + AC + DB
2AB + 2BC + 2CD + 2DA > 2CA + 2DB
Take out 2 on both the side,
2(AB + BC + CA + DA) > 2(CA + DB)
AB + BC + CA + DA > CA + DB
Hence, the given expression is true.
5. ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)
Solution –
Let us consider ABCD is quadrilateral and P is the point where the diagonals are intersect. As shown in the figure below.
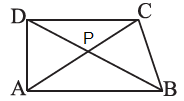
We know that,
The sum of the length of any two sides is always greater than the third side.
Now consider the ΔPAB,
Here, PA + PB > AB ———- [equation (i)]
Then, consider the ΔPBC
Here, PB + PC > BC ———- [equation (ii)]
Consider the ΔPCD
Here, PC + PD > CD ———- [equation (iii)]
Consider the ΔPDA
Here, PD + PA > DA ———- [equation (iv)]
By adding equation (i), (ii), (iii) and (iv) we get,
PA + PB + PB + PC + PC + PD + PD + PA > AB + BC + CD + DA
2PA + 2PB + 2PC + 2PD > AB + BC + CD + DA
2PA + 2PC + 2PB + 2PD > AB + BC + CD + DA
2(PA + PC) + 2(PB + PD) > AB + BC + CD + DA
From the figure we have, AC = PA + PC and BD = PB + PD
Then,
2AC + 2BD > AB + BC + CD + DA
2(AC + BD) > AB + BC + CD + DA
Hence, the given expression is true.
6. The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution –
We know that,
The sum of the length of any two sides is always greater than the third side.
From the question, it is given that two sides of triangle are 12 cm and 15 cm.
So, the third side length should be less than the sum of other two sides,
12 + 15 = 27 cm.
Then, it is given that the third side is cannot not be less than the difference of the two sides, 15 – 12 = 3 cm
So, the length of the third side falls between 3 cm and 27 cm.

Leave a Reply