NCERT Solutions Class 7 Mathematics
Chapter – 6 (The Triangle and its Properties)
The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 6 The Triangle and its Properties Exercise 6.3 has been provided here to help the students in solving the questions from this exercise.
Chapter : 6 The Triangles and its Properties
- NCERT Solution Class 7 Maths Exercise – 6.1
- NCERT Solution Class 7 Maths Exercise – 6.2
- NCERT Solution Class 7 Maths Exercise – 6.4
- NCERT Solution Class 7 Maths Exercise – 6.5
Exercise – 6.3
1. Find the value of the unknown x in the following diagrams:
(i) 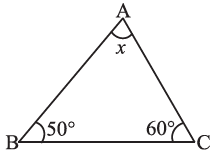 (ii)
(ii) 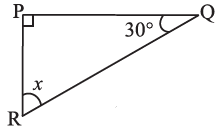 (iii)
(iii) 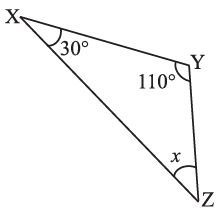
(iv) 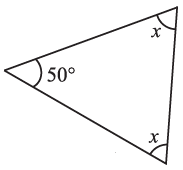 (v)
(v) 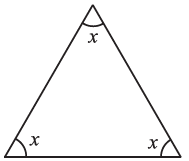 (vi)
(vi) 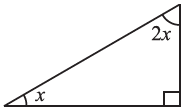
Solution –
(i) By angle sum property of a triangle, we have
∠x + 50° + 60° = 180°
⇒ ∠x + 110° = 180°
∴ ∠x = 180° – 110° = 70°
(ii) By angle sum property of a triangle, we have
∠x + 90° + 30 = 180° [∆ is right angled triangle]
⇒ ∠x + 120° = 180°
∴ ∠x – 180° – 120° = 60°
(iii) By angle sum property of a triangle, we have
∠x + 30° + 110° – 180°
⇒ ∠x + 140° = 180°
∴ ∠x = 180° – 140° = 40°
(iv) By angle sum property of a triangle, we have
∠x + ∠x + 50° = 180°
⇒ 2x + 50° = 180°
⇒ 2x = 180° – 50°
⇒ 2x = 130°
⇒ x = = 65∘
(v) By angle sum property of a triangle, we have
∠x + ∠x +∠x =180°
⇒ 3∠x = 180°
∴ ∠x = = 60∘
(vi) By angle sum property of a triangle, we have
x + 2 x + 90° = 180° (∆ is right angled triangle)
⇒ 3x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
∴ x = =30∘
2. Find the values of the unknowns x and y in the following diagrams:
(i) 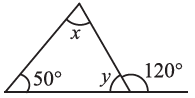 (ii)
(ii) 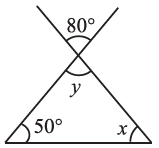 (iii)
(iii) 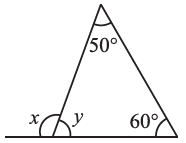
(iv) 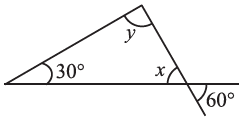 (v)
(v) 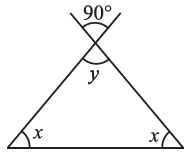 (vi)
(vi) 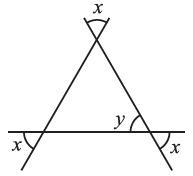
Solution –
(i) ∠x + 50° = 120° (Exterior angle of a triangle)
∴ ∠x = 120°- 50° = 70°
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
70° + ∠y + 50° = 180°
∠y + 120° = 180°
∠y = 180° – 120°
∴ ∠y = 60°
Thus ∠x = 70 and ∠y – 60°
(ii) ∠y = 80° (Vertically opposite angles are same)
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
⇒ ∠x + 80° + 50° = 180°
⇒ ∠x + 130° = 180°
∴ ∠x = 180° – 130° = 50°
Thus, ∠x = 50° and ∠y = 80°
(iii) ∠y + 50° + 60° = 180° (Angle sum property of a triangle)
∠y + 110° = 180°
∴ ∠y = 180°- 110° = 70°
∠x + ∠y = 180° (Linear pairs)
⇒ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°
Thus, ∠x = 110° and y = 70°
(iv) ∠x = 60° (Vertically opposite angles)
∠x + ∠y + 30° = 180° (Angle sum property of a triangle)
⇒ 60° + ∠y + 30° = 180°
⇒ ∠y + 90° = 180°
⇒ ∠y = 180° – 90° = 90°
Thus, ∠x = 60° and ∠y = 90°
(v) ∠y = 90° (Vertically opposite angles)
∠x + ∠x + ∠y = 180° (Angle sum property of a triangle)
⇒ 2 ∠x + 90° = 180°
⇒ 2∠x = 180° – 90°
⇒ 2∠x = 90°
∴ ∠x = = 45∘
Thus, ∠x = 45° and ∠y = 90°
(vi) From the rule of vertically opposite angles,
⇒ x = y
Then, We know that,
The sum of all the interior angles of a triangle is 180o.
⇒ x + x + x = 180o
⇒ 3x = 180o
⇒ x = = 60o

Leave a Reply