NCERT Solutions Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1

NCERT Solutions Class 10 Maths
Chapter – 8 (Introduction to Trigonometry)

The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 8 Introduction to Trigonometry Exercise 8.1 has been provided here to help the students in solving the questions from this exercise.

Chapter : 8 Introduction to Trigonometry

Exercise – 8.1

1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C

Solution – In a given triangle ABC, right angled at B = ∠B = 90°
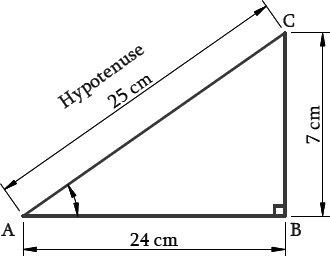
NCERT Class 10 Maths Solution

Given : AB = 24 cm and BC = 7 cm
According to the Pythagoras Theorem,
AC² = AB² + BC²= 24² + 7²
= 576 + 49 cm²
= 625 cm²
AC = 25

(i) sin A = BC/AC = 7/25
cos A = AB/AC = 24/25

(ii) sin C = AB/AC = 24/25

cos C = BC/AC = 7/25

2. In Fig. 8.13, find tan P – cot R

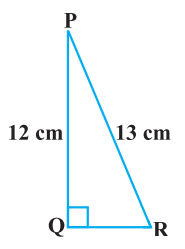
Solution – In the given ΔPQR, the given triangle is right angled at Q and the given measures are:
PR = 13cm,
PQ = 12cm
According to Pythagorean theorem,
PR² = PQ² + QR²(13 cm)² = (12 cm)² + QR²169 cm² = 144 cm² + QR²25 cm² = QR²QR = 5 cm
tan P = QR/PQ
tan P = 5/12
cot R = QR/PQ
cot R = 5/12
tan P – cot R = 5/12 – 5/12 = 0

3. If sin A = 3/4, calculate cos A and tan A.

Solution – Let us assume a right angled triangle ABC, right angled at B
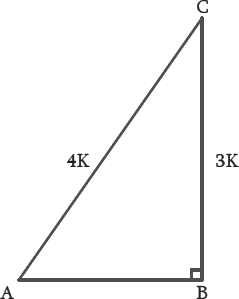
NCERT Class 10 Maths Solution
Given : Sin A = 3/4
BC/AC = 3/4
Therefore, hypotenuse AC will be 4k where k is a positive integer.
Applying Pythagoras theorem on ∆ABC, we obtain:
AC² = AB² + BC²AB² = AC² – BC²AB²= (4k)² – (3k)²AB² = 16k² – 9k²AB² = 7 k²AB = √7 k
Now, we have to find the value of cos A and tan A
cos A = AB/AC = √7k/4k = √7/4
tan A = BC/AB = 3k/√7k = 3/√7

4. Given 15 cot A = 8, find sin A and sec A.

Solution – Let us assume a right angled triangle ABC, right angled at B
NCERT Class 10 Maths Solution
Given : 15 cot A = 8
Cot A = 8/15
AB/BC = 8/15
Applying Pythagoras theorem in ΔABC, we obtain.
AC² = AB² + BC²AC² =(8k)² + (15k)²AC² = 64k² + 225k²AC² = 289k²AC = 17k
Now, we have to find the value of sin A and sec A
sin A = BC/AC = 15k/17k = 15/17
sec A = AC/AB = 17k /8k = 17/8

5. Given sec θ = 13/12 Calculate all other trigonometric ratios

Solution – Let ΔABC be a right-angled triangle, right-angled at B.

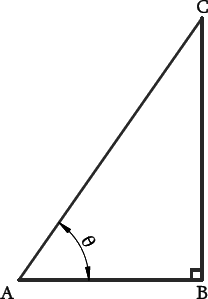
NCERT Class 10 Maths Solution
Given : sec θ = 13/12 = Hypotenuse/Adjacent side = AC/AB
Let AC be 13k and AB will be 12k
By Pythagoras theorem we get,
AC²=AB²+ BC²(13k)²= (12k)² + BC²169k²= 144k² + BC²169k²= 144k² + BC²BC^{2 =}169k² – 144k²BC²= 25k²Therefore, BC = 5k
Now, substitute the corresponding values in all other trigonometric ratios
sin θ = BC/AC = 5/13
cos θ = AB/AC = 12/13
tan θ = BC/AB = 5/12
cosec θ = AC/BC = 13/5
cot θ = AB/BC = 12/5

6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B.

Solution – Let us assume the triangle ABC in which CD ⊥ AB
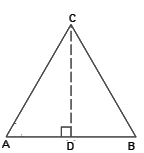
NCERT Class 10 Maths Solution
Give that the angles A and B are acute angles, such that
cos A = cos B
As per the angles taken, the cos ratio is written as
AD/AC = BD/BC
AD/BD = AC/BC
Let take a constant value
AD/BD = AC/BC = k
Now consider the equation as
AD = k.BD ———- (i)
AC = k BC ———- (ii)
By applying Pythagoras theorem in △CAD and △CBD we get,
CD² = BC² – BD²———- (iii)
CD²=AC²−AD² ———- (iv)
From the equations (iii) and (iv) we get,
AC²−AD²= BC²−BD²⇒ (kBC)² – (kBD)² = BC² – BD²
⇒ k²(BC² – BD²) = BC² – BD²
⇒ k² = 1
⇒ k = 1
Putting this value in equation (ii), we obtain
AC = BC
∠A = ∠B (Angles opposite to equal sides of a triangle are equal-isosceles triangle)

7. If cot θ = 7/8, evaluate :
(i) (1 + sin θ)(1 – sin θ)/(1+cos θ)(1-cos θ)
(ii) cot² θ

Solution – Let us assume a △ABC in which ∠B = 90° and ∠C = θ

Given :
cot θ = BC/AB = 7/8
BC = 7k
AB = 8k
According to Pythagoras theorem in △ABC we get.
AC²= AB²+BC²AC²= (8k)²+ (7k)²AC²= 64k²+ 49k²AC²= 113k²AC = √113 k
According to the sin and cos function ratios, it is written as
sin θ = AB/AC = 8k/√113k = 8/√113
cos θ = BC/AC = 7k/√113 k = 7/√113
Now apply the values of sin function and cos function:

(i) $\boldsymbol{\frac{1+sin\Theta (1-sin\Theta)}{(1+cos\Theta)(1-cos\Theta)}}$
= $\frac{(1-sin^2\Theta)}{(1-cos^2\Theta)}$
= $\frac{1-\left ( \frac{8}{\sqrt{113}} \right )^2}{1-\left ( \frac{7}{\sqrt{113}} \right )^2}$ = $\frac{113 -64}{113-49}$ = $\frac{49}{64}$

(ii) cot² θ

= $\left ( \frac{7}{8} \right )^2$ = $\frac{49}{64}$

8. If 3 cot A = 4, check whether (1-tan²A)/(1+tan² A) = cos² A – sin ²A or not.

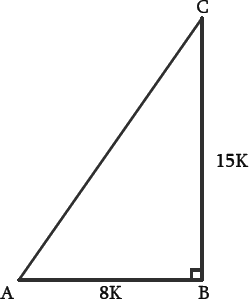
Solution – Let △ABC in which ∠B=90°
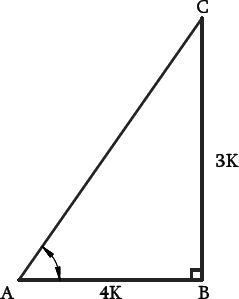
NCERT Class 10 Maths Solution
3 cot A = 4
cot A = 4/3 = AB/BC
Let AB = 4k an BC =3k,
According to the Pythagorean theorem,
AC²= AB²+ BC²AC²= (4k)²+ (3k)²AC²= 16k²+ 9k²AC²= 25k²AC = 5k
Now, apply the values corresponding to the ratios
tan A = BC/AB = 3/4
sin A = BC/AC = 3/5
cos A = AB/AC = 4/5
Now compare the left hand side(LHS) with right hand side(RHS)
L.H.S. = (1 – tan²A)/(1 + tan²A)
= (1 – (3/4)²)/(1 + (3/4)²)
= (1 – 9/16)/(1 + 9/16)
= (16 – 9)/(16 + 9)
= 7/25
R.H.S. = cos²A – sin²A
= (4/5)²– (3/4)²
=(16/25) – (9/25)
= 7/25
R.H.S. = L.H.S.
Hence,
(1 – tan²A)/(1 + tan²A) = cos²A – sin²A

9. In triangle ABC, right-angled at B, if tan A = 1/√3 find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C

Solution – Let ΔABC in which ∠B=90°
NCERT Class 10 Maths Solution
tan A = BC/AB = 1/√3
BC = 1k
AB = √3 k,
By Pythagoras theorem in ΔABC we get:
AC²= AB²+ BC²AC²= (√3 k)²+ (k)²AC²= 3k²+ k²AC²= 4k²AC = 2k
Now find the values of cos A, Sin A
Sin A = BC/AC = 1/2
Cos A = AB/AC = √3/2

Then find the values of cos C and sin C
Sin C = AB/AC = √3/2
Cos C = BC/AC = 1/2
Now, substitute the values in the given problem

(i) sin A cos C + cos A sin C
= (1/2) × (1/2 ) + √3/2 × √3/2
= 1/4 + 3/4
= 1

(ii) cos A cos C – sin A sin C
= (√3/2 )(1/2) – (1/2) (√3/2 )
= 0

10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P

Solution – In a given triangle PQR, right angled at Q, the following measures are
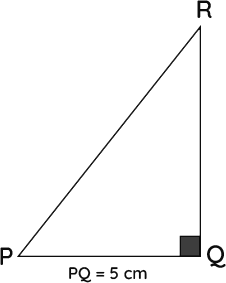
NCERT Class 10 Maths Solution
PQ = 5 cm
PR + QR = 25 cm
Now let us assume, QR = x
PR = 25 – QR
PR = 25- x
According to the Pythagorean Theorem,
PR² = PQ² + QR²Substitute the value of PR as x
(25 – x)²= 5²+ x²25² + x² – 50x = 25 + x²625 + x²-50x -25 – x²= 0
-50x = -600
x= -600/-50
x = 12 = QR
Now, find the value of PR
PR = 25 – QR
PR = 25 – 12
PR = 13
Now, substitute the value to the given problem
sin p = QR/PR = 12/13
cos p = PQ/PR = 5/13
tan p = QR/PQ = 12/5

11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.

Solution –

(i) The value of tan A is always less than 1. (False)
because tan 60^° = √3 > 1

(ii) sec A = 12/5 for some value of angle A. (True)
As hypotenuse is the largest side, the ratio on RHS will be greater than 1. Hence, the value of sec A is always greater than or equal to 1. Thus, the given statement is true.

(iii) cos A is the abbreviation used for the cosecant of angle A. (False)
Abbreviation used for cosecant of ∠A is cosec A and cos A is the abbreviation used for cosine of ∠A. Hence the given statement is false.

(iv) cot A is the product of cot and A. (False)
cot A is not the product of cot and A. It is the cotangent of ∠A. Hence, the given statement is false.

(v) sin θ = 4/3 for some angle θ. (False)
We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.

Go Back To Chapters

NCERT Solutions Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1