NCERT Solutions Class 9 Maths Chapter 1 Number Systems Ex 1.5

NCERT Solutions Class 9 Maths
Chapter – 1 (Number Systems )

The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 1 Number Systems Exercise 1.5 has been provided here to help the students in solving the questions from this exercise.

Chapter 1: Number Systems

Exercise – 1.5

1. Classify the following numbers as rational or irrational:

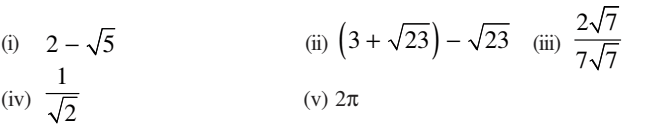
Answer –
(i) 2 –√5
Since, it is a difference of a rational and an irrational number.
∴ 2 – √5 is an irrational number.

(ii) (3 +√23) – √23
⇒ (3 + √23) – √23 = 3 + √23 – √23
= 3
which is a rational number.

(iii) $\mathbf{\frac{2\sqrt{7}}{7\sqrt{7}}}$
⇒ $\frac{2\sqrt{7}}{7\sqrt{7}}$ = $\frac{2}{7}$ , which is a rational number.

(iv) $\mathbf{\frac{1}{\sqrt{2}}}$
∵ The quotient of rational and irrational number is an irrational number.
∴ $\frac{1}{\sqrt{2}}$ is an irrational number.

(v) 2π
2π = 2 x π
∵ Product of a rational and an irrational number is an irrational number.
∴ 2π is an irrational number.

2. Simplify each of the following expressions:

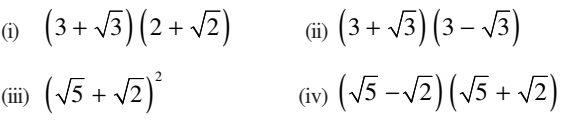
Answer –
(i) (3 + √3)(2 + √2)
⇒ 2(3 + √3) + √2(3 + √3)
⇒ 6 + 2√3 + 3√2 + √6

(ii) (3 + √3)(3 – √3 )
⇒ (3)² – (√3)²
⇒ 9 – 3
⇒ 6

(iii) (√5 + √2)²
⇒ (√5)² + (√2)² + 2(√5)(√2)
⇒ 5 + 2 + 2√10
⇒ 7 + 2√10

(iv) (√5 – √2)(√5 + √2)
⇒ (√5)² – (√2)²
⇒ 5 – 2
⇒ 3

3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter, (say d). That is, π = $\mathbf{\frac{c}{d}}$ . This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Answer – When we measure the length of a line with a scale or with any other device, we only get an approximate ational value, i.e. c and d both are irrational.
∴ $\frac{c}{d}$ is irrational and hence π is irrational.
Thus, there is no contradiction in saying that it is irrational.

4. Represent ( $\mathbf{\sqrt{9.3}}$ ) on the number line.
Answer – Let’s look into the steps below to represent $\sqrt{9.3}$ on the number line.
Step 1 – Draw a line and take AB = 9.3 units on it.
Step 2 – From B, measure a distance of 1 unit and mark C on the number line. Mark the midpoint of AC as O.
Step 3 – With ‘O’ as center and OC as radius, draw a semicircle.
Step 4 – At B, draw a perpendicular to cut the semicircle at D.
Step 5 – With B as a center and BD as radius draw an arc to cut the number line at E. Thus, taking B as the origin the distance BE = $\sqrt{9.3}$
Therefore, point E represents $\sqrt{9.3}$ on the number line.
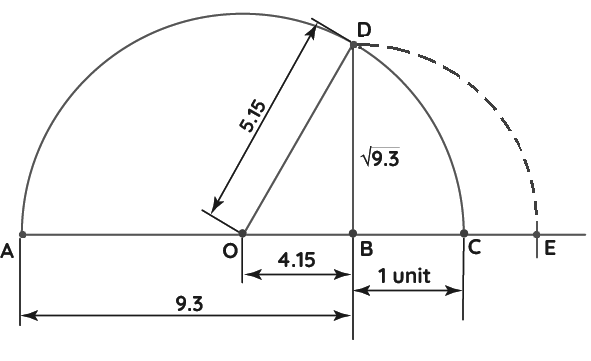
NCERT Class 9 Solutions Maths
Let’s look at the proof shown below.
AB = 9.3, BC = 1
AC = AB + BC = 10.3
OC = $\frac{AC}{2}$ = $\frac{10.3}{2}$ = 5.15
OC = OD = 5.15
OB = OC – BC = 5.15 – 1 = 4.15
In right-angled ∆OBD, using Pythagoras theorem we have,
BD² = OD² – OB²
⟹ (5.15)² – (4.15)²
⟹ (5.15 + 4.15)(5.15 – 4.15) [Using a² – b² = (a + b)(a – b)]
⟹ 9.3 × 1
⟹ 9.3
Hence, BD = $\sqrt{9.3}$ = BE [Since they are the radii of the same circle]
Thus, we can say point E represents $\sqrt{9.3}$ on the number line.

5. Rationalize the denominators of the following:

Answer –
(i) $\mathbf{\frac{1}{\sqrt{7}}}$
Multiply and divide $\frac{1}{\sqrt{7}}$ by $\sqrt{7}$

⇒ $\frac{1}{\sqrt{7}}$ × $\frac{\sqrt{7}}{\sqrt{7}}$

⇒ $\frac{\sqrt{7}}{7}$

(ii) $\mathbf{\frac{1}{\sqrt{7}-\sqrt{6}}}$
Dividing and multiplying by √7 + √6, we get
⇒ $\frac{1}{\sqrt{7}-\sqrt{6}} \times \frac{\sqrt{7} + \sqrt{6}}{\sqrt{7} + \sqrt{6}}$

⇒ $\frac{\sqrt{7}+\sqrt{6}}{(\sqrt{7})^{2}-(\sqrt{6})^{2}}$ using the property, (a + b)(a – b) = a²– b²

⇒ $\frac{\sqrt{7}+\sqrt{6}}{7-6}$

⇒ $\frac{\sqrt{7}+\sqrt{6}}{1}$

⇒ √7 + √6

(iii) $\mathbf{\frac{1}{\sqrt{5} + \sqrt{2}}}$
Dividing and multiplying by √5 – √2, we get
⇒ $\frac{1}{\sqrt{5}+\sqrt{2}} \times \frac{\sqrt{5} - \sqrt{2}}{\sqrt{5} - \sqrt{2}}$

⇒ $\frac{\sqrt{5}-\sqrt{2}}{(\sqrt{5})^{2}-(\sqrt{2})^{2}}$ using the property, (a + b)(a – b) = a²– b²

⇒ $\frac{\sqrt{5} - \sqrt{2}}{5-2}$

⇒ $\frac{\sqrt{5} - \sqrt{2}}{3}$

(iv) $\mathbf{\frac{1}{\sqrt{7}-2}}$
Multiply and divide by (√7 + 2), we get
⇒ $\frac{1}{\sqrt{7} - 2} \times \frac{\sqrt{7} + 2}{\sqrt{7} + 2}$

⇒ $\frac{\sqrt{7} + 2}{(\sqrt{7})^{2}-(2)^{2}}$ using the property, (a + b)(a – b) = a²– b²

⇒ $\frac{\sqrt{7} + 2}{7- 4}$

⇒ $\frac{\sqrt{7} + 2}{3}$

NCERT Solutions Class 9 Maths Chapter 1 Number Systems Ex 1.5