NCERT Solutions Class 8 Mathematics
Chapter – 9 (Algebraic Expressions and Identities)
The NCERT Solutions in English Language for Class 8 Mathematics Chapter – 9 Algebraic Expressions and Identities Exercise 9.2 has been provided here to help the students in solving the questions from this exercise.
Chapter 9: Algebraic Expressions and Identities
- NCERT Solution Class 8 Maths Ex – 9.1
- NCERT Solution Class 8 Maths Ex – 9.3
- NCERT Solution Class 8 Maths Ex – 9.4
- NCERT Solution Class 8 Maths Ex – 9.5
Exercise – 9.2
1. Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) – 4p, 7p
(iii) – 4p, 7pq
(iv) 4p3, – 3p
(v) 4p, 0
Solution –
(i) 4 , 7 p
= 4 × 7 × p = 28p
(ii) – 4p × 7p
= (-4 × 7 ) × (p × p )
= – 28p2
(iii) – 4p × 7pq
= (-4 × 7 ) (p × pq)
= -28p2q
(iv) 4p3 × – 3p
= (4 × -3 ) (p3 × p )
= -12p4
(v) 4p × 0
= 0
2. Find the areas of rectangles with the following pairs of monomials as their lengths and breadths, respectively.
(p, q) ; (10m, 5n) ; (20x2 , 5y2) ; (4x, 3x2) ; (3mn, 4np)
Solution –
Area of rectangle = Length x breadth.
So, it is multiplication of two monomials.
The results can be written in square units.
(i) (p, q)
Length = p
Breadth = q
∴ Area of the rectangle = Length × Breadth
= p × q
= pq
(ii) (10m, 5n)
Length = 10 m
Breadth = 5 n
∴ Area of the rectangle = Length × Breadth
= (10m) × (5n)
= (10 × 5) × (m × n)
= 50 × (mn)
= 50 mn
(iii) (20x2, 5y2)
Length = 20x2
Breadth = 5y2
∴ Area of the rectangle = Length × Breadth
= (20 × 2) × (5y2)
= (20 × 5) × (x2×y2)
= 100 × (x2y2)
= 100x2y2
(iv) (4x, 3x2)
Length = 4x
Breadth = 3x2
∴ Area of the rectangle = Length × Breadth
= (4x) × (3x2)
= (4 × 3) × (x × x2)
= 12 × x3
= 12x3
(v) (3mn, 4np)
Length = 3 mn
Breadth = 4np
∴ Area of the rectangle = Length × Breadth
= (3mn) × (4np)
= (3 × 4) × (mn) × (np)
= 12 × m × (n × n) × p
= 12mn2p
3. Complete the following table of products:
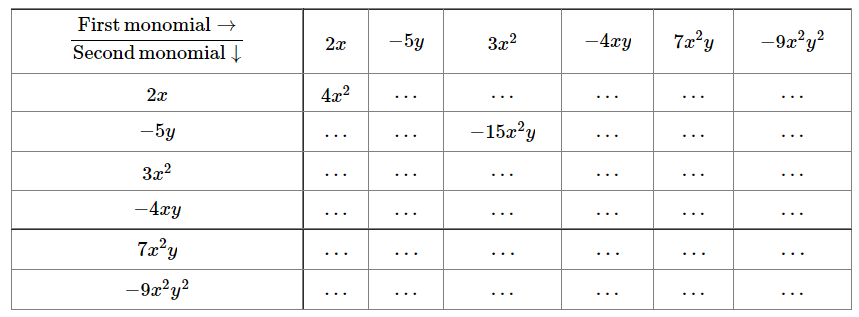
Solution –
| First monomial →
Second monomial ↓ |
2x | -5 y | 3x2 | -4xy | 7x2 y | -9x2 y2 |
| 2x | 4x2 | -10xy | 6x3 | -8x2 y | 14x3 y | -18x3 y2 |
| -5 y | -10xy | 25 y2 | -15x2 y | 20xy2 | -35x2 y2 | 45x2 y3 |
| 3x2 | 6x3 | -15x2 y | 9x4 | -12x3 y | 21x4 y | -27x4 y2 |
| -4xy | -8x2 y | 20xy2 | -12x3 y | 16x2 y2 | -28x3 y2 | 36x3 y3 |
| 7x2 y | 14x3 y | -35x2 y2 | 21x4 y | -28x3 y2 | 49x4 y2 | -63x4 y3 |
| -9x2 y2 | -18x3 y2 | 45x2 y3 | -27x4 y2 | 36x3 y3 | -63x4y3 | 81x4y4 |
4. Obtain the volume of rectangular boxes with the following length, breadth and height, respectively.
(i) 5a, 3a2, 7a4
(ii) 2p, 4q, 8r
(iii) xy, 2x2y, 2xy2
(iv) a, 2b, 3c
Solution – Volume of a rectangular box = length × breadth × height
(i) 5a, 3a2, 7a4
Volume = 5a × 3a2 × 7a4
= 5 × 3 × 7 × a × a2 × a4
= 105 a7
(ii) 2p, 4q, 8r
Volume = 2p × 4q × 8r
= 2 × 4 × 8 × p × q × r
= 64 pqr
(iii) xy, 2x2y, 2xy2
Volume = xy × 2x2 y × 2 xy2
= 2 × 2 × xy × x2 y × xy2
= 4x4 y4
(iv) a, 2b, 3c
Volume = a × 2b × 3c
= 2 × 3 × a × b × c
= 6abc
5. Obtain the product of
(i) xy, yz, zx
(ii) a, – a2 , a3
(iii) 2, 4y, 8y2 , 16y3
(iv) a, 2b, 3c, 6abc
(v) m, – mn, mnp
Solution –
(i) xy, yz, zx
= xy × yz × zx
= x2 y2 z2
(ii) a, – a2 , a3
= a × – a2 × a3
= – a6
(iii) 2, 4y, 8y2 , 16y3
= 2 × 4y × 8y2 × 16y3
= 1024y6
(iv) a, 2b, 3c, 6abc
= a × 2b × 3c × 6abc
= 36a2 b2 c2
(v) m, – mn, mnp
= m × – mn × mnp
= –m3 n2 p

Leave a Reply