NCERT Solutions Class 8 Maths Chapter 5 Data Handling Ex 5.2

NCERT Solutions Class 8 Mathematics 
Chapter – 5 (Data Handling) 

The NCERT Solutions in English Language for Class 8 Mathematics Chapter – 5 Data Handling Exercise 5.2 has been provided here to help the students in solving the questions from this exercise. 

Chapter 5: Data Handling

Exercise – 5.2 

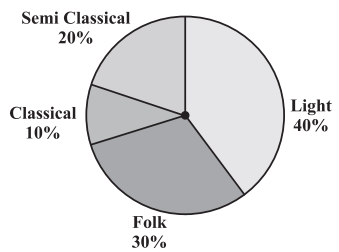
1. A survey was made to find the type of music that a certain group of young people liked in a city.
An adjoining pie chart shows the findings of this survey. From this pie chart, answer the following:
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CDs, how many of each type would they make?
NCERT Maths Solutions Class 8

Solution –

(i) 10% represents 100 people.
20% represents = \frac{100\times 20}{10} = 200
Hence, 200 young people were surveyed.

(ii) From the pie chart, it can be easily observed that the light music represents the maximum part of the pie chart (i.e. 40%).
Hence, Light music is liked by the maximum number of people.

(iii) Number of CD’s of classical music = 10% of 1000 = \frac{10\times 1000}{100} = 100

Number of CD’s of semi-classical music = 20% of 1000 = \frac{20\times 1000}{100}= 200

Number of CD’s of light music = 40% of 1000 = \frac{40\times 1000}{100} = 400

Number of CD’s of folk music = 30% of 1000 = \frac{30\times 1000}{100} = 300

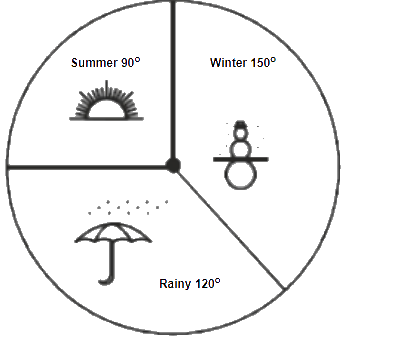
2. A group of 360 people were asked to vote for their favourite season from the three seasons rainy, winter and summer.
(i) Which season got the most votes?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information
NCERT Maths Solutions Class 8
Solution –
(i) According to the table given in the question, the winter season got the most votes.

(ii) Central angle of summer season = \frac{90\times 360}{360} = 90°

Central angle of rainy season = \frac{120\times 360}{360} = 120°

Central angle of winter season = \frac{150\times 360}{360} = 150°

(iii)
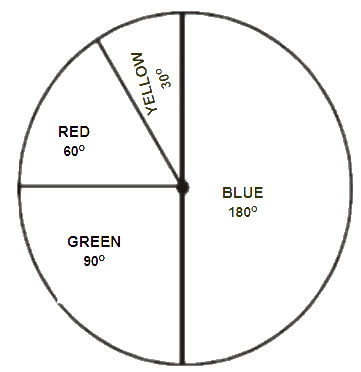
NCERT Maths Solutions Class 8

3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.
NCERT Maths Solutions Class 8
Solution – Here, central angle = 360°
Total number of people = 36

Colors No. of People Fraction  Central Angles
Blue
 18 \frac{18}{36}=\frac{1}{2} \frac{1}{2}\times 360^{\circ} =180^{\circ}
Green 9 \frac{9}{36}=\frac{1}{4} \frac{1}{4}\times 360^{\circ} =90^{\circ}
Red 6 \frac{6}{36}=\frac{1}{6} \frac{1}{6}\times 360^{\circ} =60^{\circ}
Yellow 3 \frac{3}{36}=\frac{1}{12} \frac{1}{12}\times 360^{\circ} =30^{\circ}

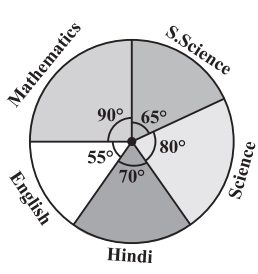
NCERT Maths Solutions Class 8

4. The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.
(i) In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi (Hint: Just study the central angles).
NCERT Maths Solutions Class 8

Solution –

Subject Central Angle (°) Marks Obtained
Mathematics
 90° \frac{90}{360}\times 540 = 135
Social Science 65° \frac{65}{360}\times 540 = 97.5
Science 80° \frac{80}{360}\times 540 = 120
Hindi 70° \frac{70}{360}\times 540 = 105
English 55° \frac{55}{360}\times 540 = 82.5

(i) The student scored 105 marks in Hindi.

(ii) Marks obtained in Mathematics = 135
Marks obtained in Hindi = 105
Difference = 135 – 105 = 30
Thus, 30 more marks were obtained by the student in Mathematics than in Hindi.

(iii) The sum of marks in Social Science and Mathematics = 97.5 + 135 = 232.5
The sum of marks in Science and Hindi = 120 + 105 = 225
∴ the sum of the marks in Social Science and Mathematics is more than in Science and Hindi.

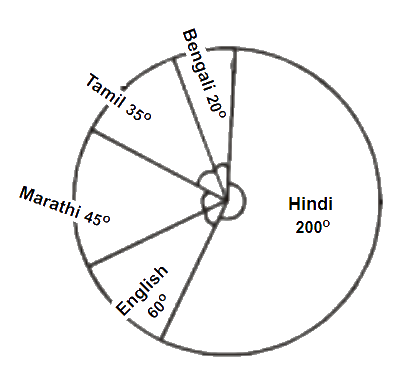
5. The number of students in a hostel speaking different languages is given below. Display the data in a pie chart.
NCERT Maths Solutions Class 8

Solution – The central angle for each language can be calculated as below:

Language Number of Students Fraction  Central Angles
Hindi
 40 \frac{40}{72}= \frac{5}{9} \frac{5}{9} \times 360^{\circ} = 200°
English 12 \frac{12}{72}= \frac{1}{6} \frac{1}{6} \times 360^{\circ} = 60°
Marathi 9 \frac{9}{72}= \frac{1}{8} \frac{1}{8} \times 360^{\circ} = 45°
Tamil 7 \frac{7}{72} \frac{7}{72} \times 360^{\circ} =  35°
Bengali 4 \frac{4}{72}= \frac{1}{18} \frac{1}{18} \times 360^{\circ} = 20°
Total 72  

Pie chart for the above data is drawn as below:
NCERT Maths Solutions Class 8

 

NCERT Class 8th Solution 
NCERT Solutions Class 8 English
NCERT Solutions Class 8 Hindi
NCERT Solutions Class 8 Mathematics 
NCERT Solutions Class 8 Sanskrit
NCERT Solutions Class 8 Science
NCERT Solutions Class 8 Social Science

You might be interested in

Admin

Leave a Reply

Your email address will not be published.

Latest from Class 8 Maths