NCERT Solutions Class 7 Maths Chapter 13 Exponents and Powers Ex 13.2

NCERT Solutions Class 7 Mathematics
Chapter – 13 (Exponents and Powers)

The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 13 Exponents and Powers Exercise 13.2 has been provided here to help the students in solving the questions from this exercise.

Chapter : 13 Exponents and Powers

Exercise – 13.2

1. Using laws of exponents, simplify and write the answer in exponential form:
(i) 3² × 3⁴ × 3⁸(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ × a²(iv) 7^x × 7²
(v) (5²)³ ÷ 5³
(vi) 2⁵ × 5⁵
(vii) a⁴ × b⁴(viii) (3⁴)³
(ix) (2²⁰ ÷ 2¹⁵) × 2³(x) 8^t ÷ 8²

Solution –

(i) 3² × 3⁴ × 3⁸By the rule of multiplying the powers with same base = a^m× aⁿ = a^{m + n}Then,
= (3)^{2 + 4 + 8}= 3¹⁴

(ii) 6¹⁵ ÷ 6¹⁰By the rule of dividing the powers with same base = a^m÷ aⁿ = a^{m – n}Then,
= (6)^{15 – 10}= 6⁵

(iii) a³ × a²By the rule of multiplying the powers with same base = a^m× aⁿ = a^{m + n}Then,
= (a)^{3 + 2}= a⁵

(iv) 7^x × 7²By the rule of multiplying the powers with same base = a^m× aⁿ = a^{m + n}Then,
= (7)^{x + 2}

(v) (5²)³ ÷ 5³By the rule of taking power of as power = (a^m)ⁿ= a^mn(5²)³ can be written as = (5)^{2 × 3}= 5⁶Now, 5⁶÷ 5³By the rule of dividing the powers with same base = a^m÷ aⁿ = a^{m – n}Then,
= (5)^{6 – 3}= 5³

(vi) 2⁵ × 5⁵By the rule of multiplying the powers with same exponents = a^m× b^m = ab^mThen,
= (2 × 5)⁵= 10⁵

(vii) a⁴ × b⁴By the rule of multiplying the powers with same exponents = a^m× b^m = ab^mThen,
= (a × b)⁴= ab⁴

(viii) (3⁴)³By the rule of taking power of as power = (a^m)ⁿ= a^mn(3⁴)³ can be written as = (3)^{4 × 3}= 3¹²

(ix) (2²⁰ ÷ 2¹⁵) × 2³By the rule of dividing the powers with same base = a^m÷ aⁿ = a^{m – n}(2²⁰ ÷ 2¹⁵) can be simplified as,
= (2)^{20 – 15}= 2⁵Then,
By the rule of multiplying the powers with same base = a^m× aⁿ = a^{m + n}2⁵ × 2³ can be simplified as,
= (2)^{5 + 3}= 2⁸

(x) 8^t ÷ 8²By the rule of dividing the powers with same base = a^m÷ aⁿ = a^{m – n}Then,
= (8)^{t – 2}

2. Simplify and express each of the following in exponential form:
(i) $\mathbf{\frac{2^3 \times 3^4\times 4}{3\times 32}}$

(ii) ((5²)³ × 5⁴) ÷ 5⁷

(iii) 25⁴ ÷ 5³

(iv) $\mathbf{\frac{3\times 7^2\times 11^8}{21\times 11^3}}$

(v) $\mathbf{\frac{3^7}{3^4\times 3^3}}$

(vi) 2⁰ + 3⁰ + 4⁰

(vii) 2⁰× 3⁰ × 4⁰

(viii) (3⁰ + 2⁰) × 5⁰

(ix) $\mathbf{\frac{2^8\times a^5}{4^3\times a^3}}$

(x) $\mathbf{\frac{a^5}{a^3} \times a^8}$

(xi) $\mathbf{\frac{4^5\times a^8b^3}{4^5\times a^5b^2}}$

(xii) (2³ × 2)²

Solution –

(i) $\mathbf{\frac{2^3 \times 3^4\times 4}{3\times 32}}$
Factors of 32 = 2 × 2 × 2 × 2 × 2
= 2⁵Factors of 4 = 2 × 2
= 2²Then,
= $\frac{2^3\times3^4\times 2^2 }{3\times 2^5}$

= $\frac{2^{3+2}\times3^4}{3\times 2^5}$ [∵ a^m× aⁿ = a^{m + n}]

= 2^{5 – 5} × 3^{4 – 1} [∵a^m÷ aⁿ = a^{m – n}]
= 2⁰ × 3³= 1 × 3³= 3³

(ii) ((5²)³ × 5⁴) ÷ 5⁷(5²)³ can be written as = (5)^{2 × 3} [∵(a^m)ⁿ= a^mn]
= 5⁶Then,
= (5⁶× 5⁴) ÷ 5⁷= (5^{6 + 4}) ÷ 5⁷ [∵a^m× aⁿ = a^{m + n}]
= 5¹⁰ ÷ 5⁷= 5^{10 – 7} [∵a^m÷ aⁿ = a^{m – n}]
= 5³

(iii) 25⁴ ÷ 5³(25)⁴ can be written as = (5 × 5)⁴= (5²)⁴(5²)⁴ can be written as = (5)^{2 × 4} [∵(a^m)ⁿ= a^mn]
= 5⁸Then,
= 5⁸ ÷ 5³= 5^{8 – 3} [∵a^m÷ aⁿ = a^{m – n}]
= 5⁵

(iv) $\mathbf{\frac{3\times 7^2\times 11^8}{21\times 11^3}}$

Factors of 21 = 7 × 3
Then,
= $\frac{3\times 7^2\times 11^8}{7\times3 \times 11^3}$

= 3^1-1 × 7^2-1 × 11^{8 – 3}= 3⁰ × 7 × 11⁵= 1 × 7 × 11⁵= 7 × 11⁵

(v) $\mathbf{\frac{3^7}{3^4\times 3^3}}$

= $\frac{3^7}{3^{4+3}}$ [∵a^m× aⁿ = a^{m + n}]

= $\frac{3^7}{3^7}$
= 3^{7 – 7} [∵a^m÷ aⁿ = a^{m – n}]
= 3⁰= 1

(vi) 2⁰ + 3⁰ + 4⁰= 1 + 1 + 1
= 3

(vii) 2⁰× 3⁰ × 4⁰= 1 × 1 × 1
= 1

(viii) (3⁰ + 2⁰) × 5⁰= (1 + 1) × 1
= (2) × 1
= 2

(ix) $\mathbf{\frac{2^8\times a^5}{4^3\times a^3}}$
(4)³ can be written as = (2 × 2)³= (2²)³(2²)³ can be written as = (2)^{2 × 3} [∵(a^m)ⁿ= a^mn]
= 2⁶Then,
= $\frac{2^8\times a^5}{2^6\times a^3}$

= 2^{8 – 6} × a^{5 – 3} [∵a^m÷ aⁿ = a^{m – n}]
= 2²× a²= 2a² [∵(a^m)ⁿ= a^mn]

(x) $\mathbf{\frac{a^5}{a^3} \times a^8}$

= (a^{5 – 3}) × a⁸ [∵a^m÷ aⁿ = a^{m – n}]
= a² × a⁸= a^{2 + 8} [∵a^m× aⁿ = a^{m + n}]
= a¹⁰

(xi) $\mathbf{\frac{4^5\times a^8b^3}{4^5\times a^5b^2}}$

= 4^{5 – 5} × (a^{8 – 5} × b^{3 – 2}) [∵a^m÷ aⁿ = a^{m – n}]
= 4⁰ × (a³b)
= 1 × a³b
= a³b

(xii) (2³ × 2)²= (2^{3 + 1})² [∵a^m× aⁿ = a^{m + n}]
= (2⁴)²(2⁴)² can be written as = (2)^{4 × 2} [∵(a^m)ⁿ= a^mn]
= 2⁸

3. Say true or false and justify your answer:
(i) 10 × 10¹¹ = 100¹¹(ii) 2³ > 5²
(iii) 2³ × 3² = 6⁵
(iv) 3²⁰ = (1000)⁰

Solution –

(i) 10 × 10¹¹ = 100¹¹LHS = 10 × 10¹¹
= 10¹⁺¹¹
= 10¹²
RHS = 100¹¹
= (10²)¹¹
= 10²²
10¹² ≠ 10²²
LHS ≠ RHS
Hence, the given statement is false.

(ii) 2³ > 5²LHS = 2³ = 8
RHS = 5²2 = 25
8 < 25
∴ 2³ < 5²LHS < RHS
2³ < 5²Hence, the given statement is false.

(iii) 2³ × 3² = 6⁵LHS = 2³× 3²
= 8 × 9
= 72
RHS = 6⁵
= 6 × 6 × 6 × 6 × 6
= 7776
∴ 72 ≠ 7776
LHS ≠ RHS
Hence, the given statement is false.

(iv) 3⁰ = (1000)⁰⇒ 1 = 1 True [∵ a⁰ = 1]
LHS = RHS
3⁰ = 1000⁰Hence, the given statement is true.

4. Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768

Solution –

(i) 108 × 192

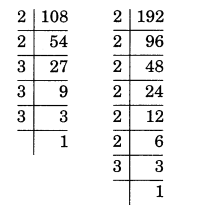
The factors of 108 = 2 × 2 × 3 × 3 × 3
= 2² × 3³The factors of 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
= 2⁶ × 3
= (2² × 3³) × (2⁶ × 3)
= 2^{2 + 6} × 3^{3 + 1} [∵a^m× aⁿ = a^{m + n}]
= 2⁸× 3⁴

(ii) 270

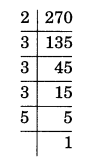
The factors of 270 = 2 × 3 × 3 × 3 × 5
= 2 × 3³ × 5

(iii) 729 × 64

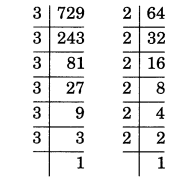
The factors of 729 = 3 × 3 × 3 × 3 × 3 × 3
= 3⁶The factors of 64 = 2 × 2 × 2 × 2 × 2 × 2
= 2⁶Then,
= (3⁶ × 2⁶)
= 3⁶ × 2⁶

(iv) 768

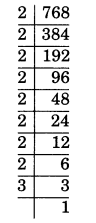
The factors of 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
= 2⁸ × 3

5. Simplify:
(i) $\mathbf{\frac{(2^5)^2 \times 7^3}{8^3\times 7}}$

(ii) $\mathbf{\frac{25\times 5^2 \times t^8}{10^3\times t^4}}$

(iii) $\mathbf{\frac{3^5\times 10^5\times 25}{5^7\times 6^5}}$

Solution –

(i) $\mathbf{\frac{(2^5)^2 \times 7^3}{8^3\times 7}}$

8³ can be written as = (2 × 2 × 2)³= (2³)³We have,

= $\frac{(2^5)^2\times 7^3}{(2^3)^3\times 7}$

= $\frac{(2^{5\times2}\times 7^3}{2^{3\times3}\times 7}$ [∵(a^m)ⁿ= a^mn]

= (2^{10 – 9} × 7^{3 – 1}) [∵a^m÷ aⁿ = a^{m – n}]
= 2 × 7²= 2 × 7 × 7
= 98

(ii) $\mathbf{\frac{25\times 5^2 \times t^8}{10^3\times t^4}}$

25 can be written as = 5 × 5
= 5²10³ can be written as = 10³= (5 × 2)³= 5³ × 2³We have,

= $\frac{5^2 \times 5^2 \times t^8}{5^3\times 2^3 \times t^4}$

= $\frac{5^{2+2} \times t^8}{5^3\times 2^3 \times t^4}$ [∵a^m× aⁿ = a^{m + n}]

= $\frac{5^{4-3} \times t^{8-4}}{2^3}$ [∵a^m÷ aⁿ = a^{m – n}]

= $\frac{5 \times t^{4}}{8}$

= $\frac{5t^4}{8}$

(iii) $\mathbf{\frac{3^5\times 10^5\times 25}{5^7\times 6^5}}$

10⁵can be written as = (5 × 2)⁵= 5⁵ × 2⁵25 can be written as = 5 × 5
= 5²6⁵ can be written as = (2 × 3)⁵= 2⁵ × 3⁵

= $\frac{3^5\times 5^5\times 2^5 \times 5^2}{5^7\times 2^5 \times 3^5}$

= $\frac{3^5\times 5^{5+2}\times 2^5}{5^7\times 2^5 \times 3^5}$ [∵a^m× aⁿ = a^{m + n}]

= (3^{5 – 5} × 5^{7 – 7}× 2^{5 – 5})
= (3⁰ × 5⁰ × 2⁰) [∵a^m÷ aⁿ = a^{m – n}]
= 1 × 1 × 1
= 1

NCERT Solutions Class 7 Maths Chapter 13 Exponents and Powers Ex 13.2

NCERT Solutions Class 7 Mathematics
Chapter – 13 (Exponents and Powers)

Exercise – 13.2

Admin

Leave a Reply Cancel reply

Latest from Class 7 Maths

NCERT Solutions Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.4

NCERT Solutions Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.3

NCERT Solutions Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.2

NCERT Solutions Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1

NCERT Solutions Class 7 Maths Chapter 14 Symmetry Ex 14.3

NCERT Solutions Class 7 Mathematics Chapter – 13 (Exponents and Powers)

Exercise – 13.2

You might be interested in

Leave a Reply Cancel reply

Latest from Class 7 Maths

NCERT Solutions Class 7 Mathematics
Chapter – 13 (Exponents and Powers)