NCERT Solutions Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1

NCERT Solutions Class 7 Mathematics 
Chapter – 13 (Exponents and Powers)

The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 13 Exponents and Powers  Exercise 13.1 has been provided here to help the students in solving the questions from this exercise. 

Chapter : 13 Exponents and Powers

• NCERT Solution Class 7 Maths Exercise – 13.2
• NCERT Solution Class 7 Maths Exercise – 13.3

Exercise – 13.1 

1. Find the value of:
(i) 2⁶
(ii) 9³
(iii) 11²
(iv) 5⁴

Solution –
(i) 2⁶
= 2 × 2 × 2 × 2 × 2 × 2
= 64

(ii) 9³
= 9 × 9 × 9
= 729

(iii) 11²
= 11 × 11
= 121

(iv) 5⁴
= 5 × 5 × 5 × 5
= 625

2. Express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c× c × d

Solution –
(i) 6 × 6 × 6 × 6
The given question can be expressed in the exponential form as 6⁴.

(ii) t × t
The given question can be expressed in the exponential form as t².

(iii) b × b × b × b
The given question can be expressed in the exponential form as b⁴.

(iv) 5 × 5× 7 × 7 × 7
The given question can be expressed in the exponential form as 5² × 7³.

(v) 2 × 2 × a × a
The given question can be expressed in the exponential form as 2² × a².

(vi) a × a × a × c × c × c × c × d
The given question can be expressed in the exponential form as a³ × c⁴ × d.

3. Express each of the following numbers using exponential notation:
(i) 512
(ii) 343
(iii) 729
(iv) 3125

Solution –
(i) 512

The factors of 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
So it can be expressed in the exponential form as 2⁹.

(ii) 343

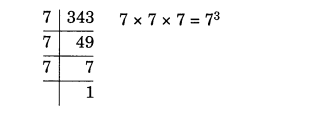
The factors of 343 = 7 × 7 × 7
So it can be expressed in the exponential form as 7³.

(iii) 729

The factors of 729 = 3 × 3 × 3 × 3 × 3 × 3
So it can be expressed in the exponential form as 3⁶.

(iv) 3125

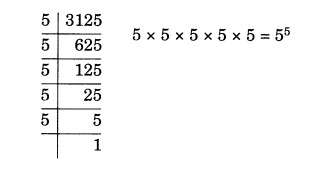
The factors of 3125 = 5 × 5 × 5 × 5 × 5
So it can be expressed in the exponential form as 5⁵.

4. Identify the greater number, wherever possible, in each of the following?
(i) 4³ or 3⁴
(ii) 5³ or 3⁵
(iii) 2⁸ or 8²
(iv) 100² or 2¹⁰⁰
(v) 2¹⁰ or 10²

Solution –

(i) 4³ or 3⁴
The expansion of 4³ = 4 × 4 × 4 = 64
The expansion of 3⁴ = 3 × 3 × 3 × 3 = 81
Clearly, 64 < 81
∴ 3⁴ is greater than 4³.

(ii) 5³ or 3⁵
The expansion of 5³ = 5 × 5 × 5 = 125
The expansion of 3⁵ = 3 × 3 × 3 × 3 × 3= 243
Clearly, 125 < 243
∴ 3⁵ is greater than 5³.

(iii) 2⁸ or 8²
The expansion of 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
The expansion of 8² = 8 × 8= 64
Clearly, 256 > 64
∴ 2⁸ is greater than 2⁸.

(iv) 100² or 2¹⁰⁰
The expansion of 100² = 100 × 100 = 10000
The expansion of 2¹⁰⁰
2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
Then,
2¹⁰⁰ = 1024 × 1024 ×1024 × 1024 ×1024 × 1024 × 1024 × 1024 × 1024 × 1024 = 1267650600228229401496703205376
Clearly, 100² < 2¹⁰⁰
∴ 2¹⁰⁰ is greater than 100².

(v) 2¹⁰ or 10²
The expansion of 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
The expansion of 10² = 10 × 10= 100
Clearly, 1024 > 100
∴ 2¹⁰ is greater than 10².

5. Express each of the following as product of powers of their prime factors:
(i) 648
(ii) 405
(iii) 540
(iv) 3600

Solution –

(i)

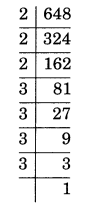
Factors of 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3
= 2³ × 3⁴

(ii) 405

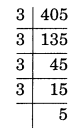
Factors of 405 = 3 × 3 × 3 × 3 × 5
= 3⁴ × 5

(iii) 540

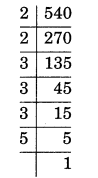
Factors of 540 = 2 × 2 × 3 × 3 × 3 × 5
= 2² × 3³ × 5

(iv) 3,600

Factors of 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 2⁴ × 3² × 5²

6. Simplify:
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × 4⁴
(v) 0 × 10²
(vi) 5² × 3³
(vii) 2⁴ × 3²
(viii) 3² × 10⁴

Solution –

(i) 2 × 10³
The above question can be written as,
= 2 × 10 × 10 × 10
= 2 × 1000
= 2000

(ii) 7² × 2²
The above question can be written as,
= 7 × 7 × 2 × 2
= 49 × 4
= 196

(iii) 2³ × 5
The above question can be written as,
= 2 × 2 × 2 × 5
= 8 × 5
= 40

(iv) 3 × 4⁴
The above question can be written as,
= 3 × 4 × 4 × 4 × 4
= 3 × 256
= 768

(v) 0 × 10²
The above question can be written as,
= 0 × 10 × 10
= 0 × 100
= 0

(vi) 5² × 3³
The above question can be written as,
= 5 × 5 × 3 × 3 × 3
= 25 × 27
= 675

(vii) 2⁴ × 3²
The above question can be written as,
= 2 × 2 × 2 × 2 × 3 × 3
= 16 × 9
= 144

(viii) 3² × 10⁴
The above question can be written as,
= 3 × 3 × 10 × 10 × 10 × 10
= 9 × 10000
= 90000

7. Simplify:
(i) (– 4)³
(ii) (-3) × (-2)³
(iii) (-3)² × (-5)²
(iv) (-2)³ × (-10)³

Solution –

(i) (– 4)³
The expansion of -4³
= – 4 × – 4 × – 4
= – 64

(ii) (–3) × (–2)³
The expansion of (-3) × (-2)³
= – 3 × – 2 × – 2 × – 2
= – 3 × – 8
= 24

(iii) (–3)² × (–5)²
The expansion of (-3)² × (-5)²
= – 3 × – 3 × – 5 × – 5
= 9 × 25
= 225

(iv) (–2)³ × (–10)³
The expansion of (-2)³ × (-10)³
= – 2 × – 2 × – 2 × – 10 × – 10 × – 10
= – 8 × – 1000
= 8000

8. Compare the following numbers:
(i) 2.7 × 10¹² ; 1.5 × 10⁸
(ii) 4 × 10¹⁴; 3 × 10¹⁴

Solution –

(i) 2.7 × 10¹² ; 1.5 × 10⁸
Here, 10¹² > 10⁸
∴ 2.7 × 10¹²> 1.5 × 10⁸

(ii) 4 × 10¹⁴ ; 3 × 10¹⁷
Here, 10¹⁷ > 10¹⁴
∴ 4 × 10¹⁴ < 3 × 10¹⁷