NCERT Solutions Class 6 Maths Chapter 7 Fractions Ex 7.6

NCERT Solutions Class 6 Maths
Chapter – 7 (Fractions)

The NCERT Solutions in English Language for Class 6 Mathematics Chapter – 7 Fractions Exercise 7.6 has been provided here to help the students in solving the questions from this exercise.

Chapter 7: Fractions

Exercise – 7.6

1. Solve.
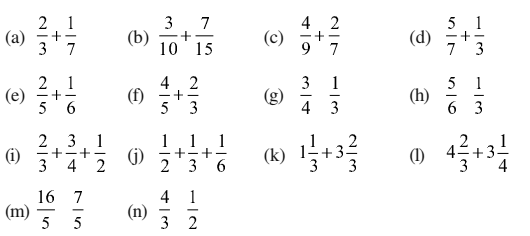
$NCERT Class 6 Math Solution$

Solution :
(a) $\frac{2}{3} + \frac{1}{7}$
LCM of 3 and 7 = 21
$\therefore \frac{2\times 7}{3\times7} +\frac{1\times3}{7\times3} = \frac{14}{21} + \frac{3}{21}$

= $\frac{17}{21}$

(b) $\frac{3}{10} + \frac{7}{15}$

LCM of 10 and 15 = 30

$\therefore \frac{3\times3}{10\times3} +\frac{7\times2}{15\times2} = \frac{9}{30} + \frac{14}{30}$

= $\frac{23}{30}$

(c) $\frac{4}{9} + \frac{2}{7}$

LCM of 9 and 7 = 63

$\therefore \frac{4\times 7}{9\times 7} +\frac{2\times 9}{7\times 9} = \frac{28}{63} +\frac{18}{63}$

= $\frac{46}{63}$

(d) $\frac{5}{7} +\frac{1}{3}$

LCM of 7 and 3 = 21

$\therefore \frac{5\times 3}{7\times 3}+\frac{1\times 7}{3\times 7} = \frac{15}{21} +\frac{7}{21}$

= $\frac{22}{21}$

(e) $\frac{2}{5} + \frac{1}{6}$

LCM of 5 and 6 = 30

$\therefore \frac{2\times 6}{5\times 6} +\frac{1\times 5}{6\times 5} = \frac{12}{30} +\frac{5}{30}$

= $\frac{17}{30}$

(f) $\frac{4}{5} + \frac{2}{3}$

LCM of 5 and 3 = 15

$\therefore \frac{4\times 3}{5\times 3} +\frac{2\times 5}{3\times 5} = \frac{12}{15} +\frac{10}{15}$

= $\frac{22}{15}$

(g) $\frac{3}{4} - \frac{1}{3}$

LCM of 4 and 3 = 12

$\therefore \frac{3\times 3}{4\times 3} - \frac{1\times 4}{3\times 4} = \frac{9}{12} - \frac{4}{12}$

$\frac{9-4}{12} = \frac{5}{12}$

(h) $\frac{5}{6}-\frac{1}{3}$

LCM of 6 and 3 = 6

$\therefore \frac{5\times 1}{6\times1} - \frac{1\times2}{3\times2} = \frac{5}{6} - \frac{2}{6} = \frac{5-2}{6}$

$\frac{3}{6} = \frac{3 \div 3}{6\div3} = \frac{1}{2}$

(i) $\frac{2}{3} +\frac{3}{4} +\frac{1}{2}$

LCM of 3, 4 and 2 = 12

$\therefore \frac{2\times4}{3\times4} +\frac{3\times3}{4\times3} + \frac{1\times6}{2\times6}$

= $\frac{8}{12} + \frac{9}{12}+ \frac{6}{12} = \frac{8+9+6}{12} = \frac{23}{12}$

(j) $\frac{1}{2} + \frac{1}{3} + \frac{1}{6}$

LCM of 2, 3 and 6 = 6

$\therefore \frac{1\times3}{2\times3} + \frac{1\times2}{3\times2} + \frac{1\times1}{6\times1} = \frac{3}{6} +\frac{2}{6} +\frac{1}{6}$

= $\frac{3 + 2+1}{6} = \frac{6}{6} = 1$

(k) $1\frac{1}{3} + 3\frac{2}{3} = \frac{3\times1+1}{3} + \frac{3\times3+2}{3} = \frac{4}{3} + \frac{11}{3}$

$\therefore \frac{4 + 11}{3} = \frac{15}{3} = \frac{15 \div 3}{ 3 \div 3} = 5$

(l) $4\frac{2}{3} + 3\frac{1}{4} = \frac{3\times4+2}{3} + \frac{4\times3 +1}{4} = \frac{14}{3} + \frac{13}{4}$

LCM of 3 and 4 = 12

$\frac{14\times4}{3\times4} +\frac{13\times3}{4\times3}$ = $\frac{56}{12} + \frac{39}{12} = \frac{56 +39}{12} = \frac{95}{12}$

(m) $\frac{16}{5} - \frac{7}{5}$

$\frac{16-7}{5} = \frac{9}{5}$

(n) $\frac{4}{3} - \frac{1}{2}$

LCM of 3 and 2 = 6

$\therefore \frac{4\times2}{3\times2} -\frac{1\times3}{2\times3} = \frac{8}{6} - \frac{3}{6}$

$\frac{8-3}{6} = \frac{5}{6}$

2. Sarita bought $\mathbf{\frac{2}{5}}$ metre of ribbon and Lalita $\mathbf{\frac{3}{4}}$ metre of ribbon. What is the total length of the ribbon they bought?

Solution:

Length of ribbon bought by Sarita = $\frac{2}{5}$ metre

Length of ribbon bought by Lalita = $\frac{3}{4}$ metre
∴ Length of ribbon bought by Sarita and Lalita = $\frac{2}{5} + \frac{3}{4}$

LCM of 5 and 4 = 20

$\therefore \frac{2\times 4}{5\times4} + \frac{3\times5}{4\times5} = \frac{8}{20} + \frac{15}{20} = \frac{23}{20}$

Hence, the required length = $\frac{23}{20}$ metre.

3. Naina was given $\mathbf{1\frac{1}{2}}$ piece of cake and Najma was given $\mathbf{1\frac{1}{3}}$ piece of cake. Find the total amount of cake was given to both of them.

Solution :

Piece of cake given to Naina = $1\frac{1}{2}$

Piece of cake given to Najma = $1\frac{1}{3}$

Piece of cake given to Naina and Najma = $1\frac{1}{2}$ + $1\frac{1}{3}$

$\frac{2\times 1 + 1}{2} + \frac{3\times 1+1}{3} = \frac{3}{2} + \frac{4}{3}$

LCM of 2 and 3 = 6

$\therefore \frac{3\times 3}{2\times3} + \frac{4\times2}{3\times2} = \frac{9}{6} + \frac{8}{6} = \frac{17}{6}$ $= 2\frac{5}{6}$

Hence the total amount of piece given to both $= 2\frac{5}{6}$

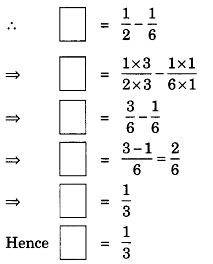
4. Fill in the boxes:
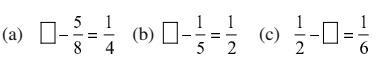
$NCERT Class 6 Math Solution$

Solution :

(a) $\square - \frac{5}{8} = \frac{1}{4}$

Here, missing number is $\frac{1}{4}$ more than $\frac{5}{8}$ .
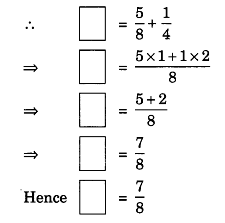
$NCERT Class 6 Math Solution$

(b) $\square - \frac{1}{5} = \frac{1}{2}$

Here, missing number is $\frac{1}{2}$ more than $\frac{1}{5}$ .
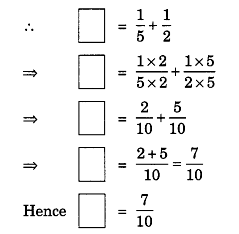
$NCERT Class 6 Math Solution$

(c) $\frac{1}{2} - \square = \frac{1}{6}$

Here, missing number is $\frac{1}{6}$ less than $\frac{1}{2}$ .
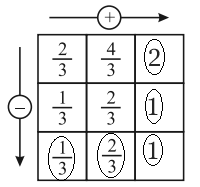
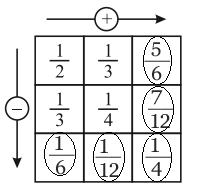
$NCERT Class 6 Math Solution$

5. Complete the addition-subtraction box.
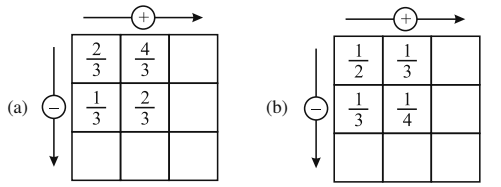
$NCERT Class 6 Math Solution$

Solution :

$NCERT Class 6 Math Solution$

Thus the box may be completed as follows:
$NCERT Class 6 Math Solution$

$NCERT Class 6 Math Solution$
Thus the box may be completed as follows:
$NCERT Class 6 Math Solution$

6. A piece of wire $\mathbf{\frac{7}{8}}$ metre long broke into two pieces. One piece was $\mathbf{\frac{1}{4}}$ metre long. How long is the other piece?

Solution :

Total length of the wire = $\frac{7}{8}$ metre
Length of one piece of wire = $\frac{1}{4}$ metre

∴ Length of the other piece = $\frac{7}{8}$ – $\frac{1}{4}$
LCM of 8 and 4 = 8

$\therefore \frac{7}{8} - \frac{1\times 2}{4\times 2} = \frac{7}{8} - \frac{2}{8} = \frac{7-2}{8} = \frac{5}{8}$

Hence, the length of the other piece = $\frac{5}{8}$ metre.

7. Nandini’s house is $\mathbf{\frac{9}{10}}$ km from her school. She walked some distance and then took a bus for $\mathbf{\frac{1}{2}}$ km to reach the school. How far did she walk?

Solution:

Total distance from house to school = $\frac{9}{10}$ km.

Distance travelled by Nandini by bus = $\frac{1}{2}$ km
∴ Distance travelled by her on foot = $\frac{9}{10}$ – $\frac{1}{2}$
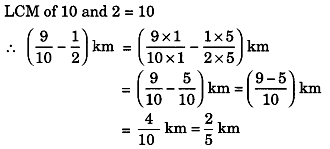
$NCERT Class 6 Math Solution$
Hence, the distance travelled by her on foot = $\frac{2}{5}$ km.

8. Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is $\mathbf{\frac{5}{6}}$ th full and Samuel’s shelf is $\mathbf{\frac{2}{5}}$ th full. Whose bookshelf is more full? By what fraction?

Solution:

Asha’s shelf is $\frac{5}{6}$ th full
and Samuel’s shelf is $\frac{2}{5}$ th full
Comparing $\frac{5}{6}$ and $\frac{2}{5}$
LCM of 6 and 5 = 30

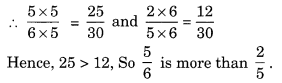
Hence, Asha’s shelf is full more than Samuel’s shelf.

Hence, $\frac{13}{30}$ th fraction is more full of Asha’s shelf.

9. Jaidev takes $\mathbf{2\frac{1}{5}}$ minutes to walk across the school ground. Rahul takes $\mathbf{\frac{7}{4}}$ minutes to do the same. Who takes less time and by what fraction?

Solution :

Time taken by Jaidev to walk across the school ground = $2\frac{1}{5}$ minutes = $\frac{11}{5}$ minutes
Time taken by Rahul to walk across the school ground = $\frac{7}{4}$ minutes
Comparing $\frac{11}{5}$ minutes and $\frac{7}{4}$ minutes.

So, the time take to cover the same distance by Rahul is less than that of Jaidev.

Hence, Rahul takes $\frac{9}{20}$ minutes less to across the school ground.

NCERT Class 6^thSolution

NCERT Solutions Class 6 English

NCERT Solutions Class 6 Hindi

NCERT Solutions Class 6 Maths

NCERT Solutions Class 6 Sanskrit

NCERT Solutions Class 6 Science

NCERT Solutions Class 6 Social Science

NCERT Solutions Class 6 Maths Chapter 7 Fractions Ex 7.6