NCERT Solutions Class 6 Maths Chapter 7 Fractions Ex 7.3

NCERT Solutions Class 6 Maths
Chapter – 7 (Fractions)

The NCERT Solutions in English Language for Class 6 Mathematics Chapter – 7 Fractions Exercise 7.3 has been provided here to help the students in solving the questions from this exercise.

Chapter 7: Fractions

Exercise – 7.3

1. Write the fractions. Are all these fractions equivalent?
(a) 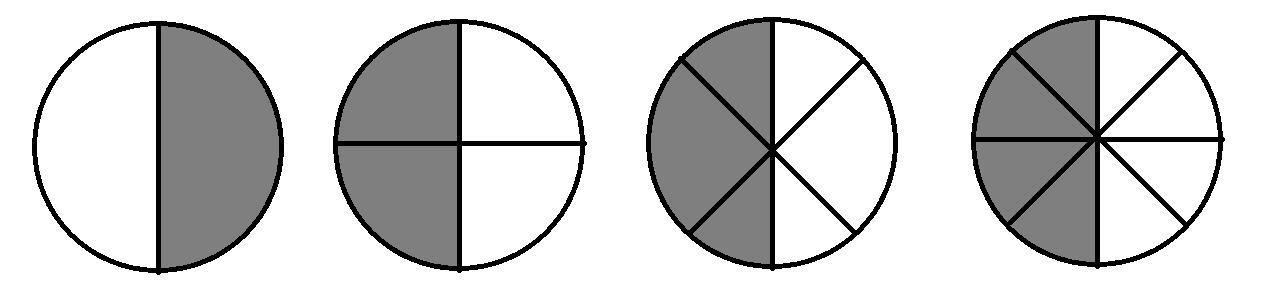$NCERT Class 6 Math Solution$

(b) $NCERT Class 6 Math Solution$

Solutions:

(a)
(i) The shaded portion is $\frac{1}{2}$

(ii) The shaded portion is $\frac{2}{4} = \frac{2\div 2}{4\div 2} = \frac{1}{2}$

(iii) The shaded portion is $\frac{3}{6} = \frac{3\div 3}{6\div 3} = \frac{1}{2}$

(iv) The shaded portion is $\frac{4}{8} = \frac{4\div 4}{8\div 4} = \frac{1}{2}$
Hence, all fractions are equivalent.

(b)
(i) The shaded portion is $\frac{4}{12} = \frac{4\div 4}{12\div 4} = \frac{1}{3}$

(ii)The shaded portion is $\frac{3}{9} = \frac{3\div 3}{9\div 3} = \frac{1}{3}$

(iii) The shaded portion is $\frac{2}{6} = \frac{2\div 2}{6\div 2} = \frac{1}{3}$

(iv) The shaded portion is $\frac{1}{3}$

(v) The shaded portion is $\frac{6}{15} = \frac{6\div 3}{15\div 3} = \frac{2}{5}$
All the fractions in their simplest form are not equal.
Hence, they are not equivalent fractions.

2. Write the fractions and pair up the equivalent fractions from each row.
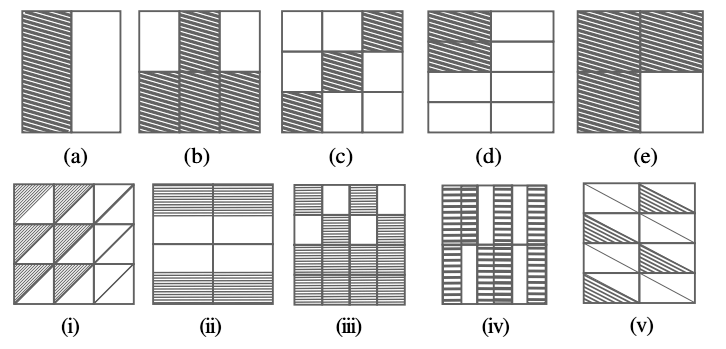
$NCERT Class 6 Math Solution$

Solutions:

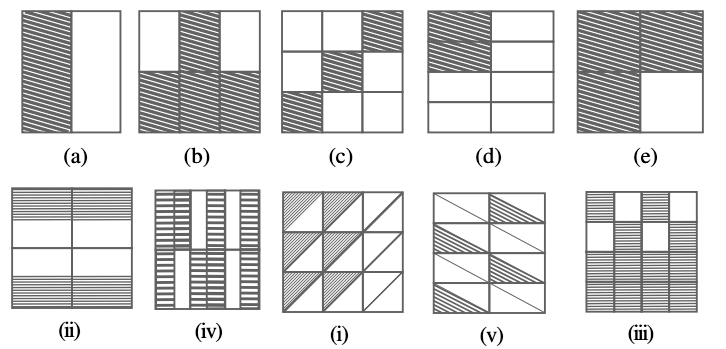
$NCERT Class 6 Math Solution$

(a) $\frac{1}{2}$	(ii) $\frac{4}{8} = \frac{4\div 4}{8\div 4} = \frac{1}{2}$
(b) $\frac{4}{6} = \frac{4\div 2}{6\div 2} = \frac{2}{3}$	(iv) $\frac{8}{12} = \frac{8\div 4}{12\div 4} = \frac{2}{3}$
(c) $\frac{3}{9} = \frac{3\div 3}{9\div 3} = \frac{1}{3}$	(i) $\frac{6}{18} = \frac{6\div 6}{18\div 6} = \frac{1}{3}$
(d) $\frac{2}{8} = \frac{2\div 2}{8\div 2} = \frac{1}{4}$	(v) $\frac{4}{16} = \frac{4\div 4}{16\div 4} = \frac{1}{4}$
(e) $\frac{3}{4}$	(iii) $\frac{12}{16} = \frac{12\div 4}{16\div 4} = \frac{3}{4}$

3. Replace ☐ in each of the following by the correct number:
(a) $\frac{2}{7} = \frac{8}{\square }$

(b) $\frac{5}{8} = \frac{10}{\square }$

(d) $\frac{45}{60} = \frac{15}{\square}$

(e) $\frac{18}{24} = \frac{\square}{4}$

Solutions:

(a) Given
$\frac{2}{7} = \frac{8}{\square }$
2 × ☐ = 7 × 8
$\square = \frac{7\times 8}{2} = \frac{7\times 8 \div 2}{2\div 2}= 7\times 4$
= 28

(b) Given
$\frac{5}{8} = \frac{10}{\square }$

$\square = \frac{8\times 10}{5} = \frac{8\times 10 \div 5}{5\div 5}= 8\times 2$
= 16

(c) Given
$\frac{3}{5} = \frac{\square }{20}$

3 × 20 = ☐ x 5

$\square = \frac{3\times 20}{5} = \frac{3\times 20 \div 5}{5\div 5}= 3\times 4$
= 12

(d) Given
$\frac{45}{60} = \frac{15}{\square}$

45 x ☐ = 15 × 60

$\square = \frac{15\times 60}{45} = \frac{15\times 60 \div 15}{45\div 15}= \frac{60}{3}$

$\square = \frac{60 \div 3}{3 \div 3}$
= 20

(e) Given
$\frac{18}{24} = \frac{\square}{4}$

18 × 4 = ☐ x 24

$\square = \frac{18 \times 4}{24}= \frac{18 \times 4 \div 4}{24\div 4}$
$\square = \frac{18}{6} = \frac{18\div 6}{6\div 6}$
= 3

4. Find the equivalent fraction of $\mathbf{\frac{3}{5}}$ having
(a) denominator 20
(b) numerator 9
(c) denominator 30
(d) numerator 27

Solutions:

(a) We require denominator 20
$\frac{\square }{20} = \frac{3}{5} \Rightarrow \square = \frac{3 \times 20}{5}$

$\square = \frac{3 \times 20 \div 5}{5\div5} \Rightarrow 3\times 4$
= 12
Therefore the required fraction is $\frac{12}{20}$

(b) We require numerator 9
Let ☐ be the denominator of the fractions
$\therefore \frac{9}{\square} = \frac{3}{5} \Rightarrow \square \times 3 = 9 \times 5$

$\square = \frac{9 \times 5 \div 3}{3\div3} \Rightarrow 3\times 5$
= 15
Therefore the required fraction is $\frac{9}{15}$

(c) We require denominator 30
Let ☐ be the numerator of the fraction

$\therefore \frac{\square }{30} = \frac{3}{5} \Rightarrow \square = \frac{3 \times 30}{5}$
$\square = \frac{3 \times 30 \div 5}{5\div5} \Rightarrow 3\times 6$
= 18

Therefore the required fraction is $\frac{18}{30}$

(d) We require numerator 27
Let ☐ be the denominator of the fraction

$\frac{27}{\square} = \frac{3}{5} \Rightarrow \square \times 3 = 27 \times 5$

$\square = \frac{27 \times 5 \div 3}{3\div3} \Rightarrow 9\times 5$
= 45

Therefore the required fraction is $\frac{27}{45}$

5. Find the equivalent fraction of $\mathbf{\frac{36}{48}}$ with
(a) numerator 9
(b) denominator 4

Solutions:

(a) Given numerator = 9
$\therefore \frac{9}{A} = \frac{36}{48}\Rightarrow A \times 36 = 9 \times 48$

$A = \frac{9 \times 48}{36} \Rightarrow \frac{9 \times 48 \div 12}{36 \div 12}$

$A = \frac{9 \times 4}{3} \Rightarrow \frac{9 \times 4 \div 3}{3 \div 3}$
A = 3 x 4
A = 12
Hence, the equivalent fraction is $\frac{9}{12}$

(b) Given, denominator = 4

$\therefore \frac{N}{4} = \frac{36}{48}\Rightarrow N \times 48 = 4 \times 36$

$N = \frac{4 \times 36}{48} \Rightarrow \frac{4 \times 36 \div 12}{48 \div 12} \Rightarrow \frac{4 \times 3}{4}$

$N = \frac{4 \times 3 \div 4}{4 \div 4}$
N = 3
Hence, the equivalent fraction is $\frac{3}{4}$

6. Check whether the given fractions are equivalent:
(a) $\frac{5}{9}, \frac{30}{54}$

(b) $\frac{3}{10}, \frac{12}{50}$

Solutions:

(a) Given $\frac{5}{9}$ and $\frac{30}{54}$

We have 5 × 54 = 270
9 × 30 = 270
270 = 270

Hence, $\frac{5}{9}$ and $\frac{30}{54}$ are equivalent fractions

(b) Given $\frac{3}{10}$ and $\frac{12}{50}$

We have 3 × 50 = 150
10 × 12 = 120
150 ≠ 120

Hence, $\frac{3}{10}$ and $\frac{12}{50}$ are not equivalent fractions

(c) Given $\frac{7}{13}$ and $\frac{5}{11}$

We have 7 × 11 = 77
5 × 13 = 65
77 ≠ 65

Hence, $\frac{7}{13}$ and $\frac{5}{11}$ are not equivalent fractions

7. Reduce the following fractions to simplest form:
(a) $\frac{48}{60}$

(b) $\frac{150}{60}$

(d) $\frac{12}{52}$

(e) $\frac{7}{28}$

Solutions:

(a) $\frac{48}{60} = \frac{12 \times 4}{12 \times 5} = \frac{4}{5}$

(b) $\frac{150}{60} = \frac{30 \times 5}{30 \times 2} = \frac{5}{2}$

(c) $\frac{84}{98} = \frac{14 \times 6}{14 \times 7} = \frac{6}{7}$

(d) $\frac{12}{52} = \frac{4 \times 3}{4 \times 13} = \frac{3}{13}$

(e) $\frac{7}{28} = \frac{7 \times 1}{7 \times 4} = \frac{1}{4}$

8. Ramesh had 20 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up 10 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each use up? Check if each has used up an equal fraction of her/his pencils?

Solutions:

Total number of pencils Ramesh had = 20
Number of pencils used by Ramesh = 10
∴ Fraction = $\frac{10}{20} = \frac{1}{2}$

Total number of pencils Sheelu had = 50
Number of pencils used by Sheelu = 25
∴ Fraction = $\frac{25}{50} = \frac{1}{2}$

Total number of pencils Jamaal had = 80
Number of pencils used by Jamaal = 40
∴ Fraction = $\frac{40}{80} = \frac{1}{2}$

Yes, each has used up an equal fraction of pencils i.e $\frac{1}{2}$

9. Match the equivalent fractions and write two more for each.

(i) $\frac{250}{400}$	(a) $\frac{2}{3}$
(ii) $\frac{180}{200}$	(b) $\frac{2}{5}$
(iii) $\frac{660}{990}$	(c) $\frac{1}{2}$
(iv) $\frac{180}{360}$	(d) $\frac{5}{8}$
(v) $\frac{220}{550}$	(e) $\frac{9}{10}$

Solutions:

(i) $\frac{250}{400} = \frac{50 \times 5}{50 \times 8}= \frac{5}{8}$

$\frac{10}{16} and \frac{15}{24}$ are two more fractions

(ii) $\frac{180}{200} = \frac{20 \times 9}{20 \times 10}= \frac{9}{10}$

$\frac{18}{20} and \frac{27}{30}$ are two more fractions

(iii) $\frac{660}{990} = \frac{330 \times 2}{330 \times 3}= \frac{2}{3}$

$\frac{200}{300} and \frac{400}{600}$ are two more fractions

(iv) $\frac{180}{360} = \frac{180 \times 1}{180 \times 2}= \frac{1}{2}$

$\frac{20}{40}and \frac{30}{60}$ are two more fractions

(v) $\frac{220}{550} = \frac{110 \times 2}{110 \times 5}= \frac{2}{5}$

$\frac{20}{50} and \frac{200}{500}$ are two more fractions

∴ The equivalent fractions are

(i) $\frac{250}{400}$	(d) $\frac{5}{8}$
(ii) $\frac{180}{200}$	(e) $\frac{9}{10}$
(iii) $\frac{660}{990}$	(a) $\frac{2}{3}$
(iv) $\frac{180}{360}$	(c) $\frac{1}{2}$
(v) $\frac{220}{550}$	(b) $\frac{2}{5}$

NCERT Class 6^thSolution

NCERT Solutions Class 6 English

NCERT Solutions Class 6 Hindi

NCERT Solutions Class 6 Maths

NCERT Solutions Class 6 Sanskrit

NCERT Solutions Class 6 Science

NCERT Solutions Class 6 Social Science

NCERT Solutions Class 6 Maths Chapter 7 Fractions Ex 7.3