NCERT Solutions Class 10 Maths
Chapter – 7 (Coordinate Geometry)
The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 7 Coordinate Geometry Exercise 7.4 has been provided here to help the students in solving the questions from this exercise.
Chapter : 7 Coordinate Geometry
- NCERT Class 10 Maths Solution Ex – 7.1
- NCERT Class 10 Maths Solution Ex – 7.2
- NCERT Class 10 Maths Solution Ex – 7.3
Exercise – 7.4
1. Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A (2, –2) and B (3, 7).
Solution – Consider line 2x + y – 4 = 0 divides line AB joined by the two points A(2, -2) and B(3, 7) in k : 1 ratio.
Coordinates of point of division can be given as follows:
x =
y =
Substituting the values of x and y given equation, i.e. 2x + y – 4 = 0, we have
2 +
– 4 = 0
= 4
4 + 6k – 2 + 7k = 4(k+1)
-2 + 9k = 0
k = 2/9
Hence, the ratio is 2 : 9.
2. Find the relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution – If given points are collinear, then the area of the triangle formed by them must be zero.
Let (x, y), (1, 2) and (7, 0) are vertices of a triangle,
Area of a triangle = × [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
[x(2 – 0) + 1 (0 – y) + 7( y – 2)] = 0
2x – y + 7y – 14 = 0
2x + 6y – 14 = 0
x + 3y – 7 = 0.
Which is the required result.
3. Find the centre of a circle passing through points (6, -6), (3, -7) and (3, 3).
Solution – Let A = (6, -6), B = (3, -7), and C = (3, 3) are the points on a circle.
If O is the centre, then OA = OB = OC (radii are equal)
If O = (x, y), then
OA = √[(x – 6)2 + (y + 6)2]
OB = √[(x – 3)2 + (y + 7)2]
OC = √[(x – 3)2 + (y – 3)2]
Choose : OA = OB, we have
After simplifying above, we get -6x = 2y – 14 ——————- (i)
Similarly, OB = OC
(x – 3)2 + (y + 7)2 = (x – 3)2 + (y – 3)2
(y + 7)2 = (y – 3)2
y2 + 14y + 49 = y2 – 6y + 9
20y = -40
y = -2
Substituting the value of y in equation (i), we get
-6x = 2y – 14
-6x = -4 – 14 = -18
x = 3
Hence, the centre of the circle is located at point (3, -2).
4. The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
Solution – Let ABCD is a square, where A(-1,2) and B(3,2). And Point O is the point of intersection of AC and BD.
To Find: Coordinate of points B and D.
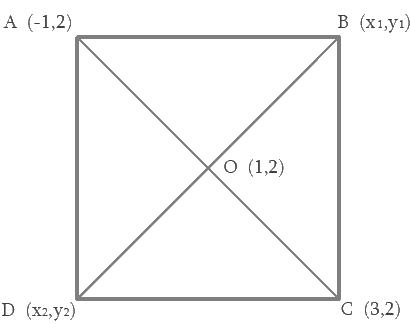
Step 1: Find the distance between A and C and the coordinates of point O.
We know that the diagonals of a square are equal and bisect each other.
AC = √[(3 + 1)2 + (2 – 2)2] = 4
Coordinates of O can be calculated as follows:
x = (3 – 1)/2 = 1
y = (2 + 2)/2 = 2
So, O(1, 2)
Step 2: Find the side of the square using the Pythagoras theorem
Let a be the side of the square and AC = 4
From the right triangle, ACD,
a = 2√2
Hence, each side of the square = 2√2
Step 3: Find the coordinates of point D
Equate the length measure of AD and CD
Say, if the coordinates of D are (x1, y1)
AD = √[(x1 + 1)2 + (y1 – 2)2]
Squaring both sides,
AD2 = (x1 + 1)2 + (y1 – 2)2
CD2 = (x1 – 3)2 + (y1 – 2)2
Since all sides of a square are equal, which means AD = CD
(x1 + 1)2 + (y1 – 2)2 = (x1 – 3)2 + (y1 – 2)2
x12 + 1 + 2x1 = x12 + 9 – 6x1
8x1 = 8
x1 = 1
The value of y1 can be calculated as follows by using the value of x.
From step 2: each side of the square = 2√2
CD2 = (x1 – 3)2 + (y1 – 2)2
8 = (1 – 3)2 + (y1 – 2)2
8 = 4 + (y1 – 2)2
y1 – 2 = 2
y1 = 4
Hence, D = (1, 4)
Step 4: Find the coordinates of point B
From line segment, BOD
Coordinates of B can be calculated using coordinates of O, as follows:
Earlier, we had calculated O = (1, 2)
Say B = (x2, y2)
For BD:
1 = (x2 + 1)/2
x2 = 1
2 = (y2 + 4)/2
y2 = 0
Therefore, the coordinates of required points are B = (1,0) and D = (1,4)
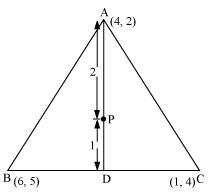
5. The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular lawn in the plot, as shown in fig. 7.14. The students are to sow the seeds of flowering plants on the remaining area of the plot.
(i) Taking A as the origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of triangle PQR if C is the origin?
Also, calculate the areas of the triangles in these cases. What do you observe?

Solution –
(i) Taking A as the origin, the coordinates of the vertices P, Q and R are,
From figure: P = (4, 6), Q = (3, 2), R (6, 5)
Here, AD is the x-axis and AB is the y-axis.
(ii) Taking C as the origin,
The coordinates of vertices P, Q and R are ( 12, 2), (13, 6) and (10, 3), respectively.
Here, CB is the x-axis and CD is the y-axis.
Find the area of triangles:
Area of triangle PQR in case of origin A:
Using formula: Area of a triangle = 1/2 × [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= ½ [4(2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
= ½ (- 12 – 3 + 24 )
= 9/2 sq unit
(iii) Area of triangle PQR in case of origin C:
Area of a triangle = 1/2 × [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= ½ [ 12(6 – 3) + 13 ( 3 – 2) + 10( 2 – 6)]
= ½ ( 36 + 13 – 40)
= 9/2 sq unit
This implies, Area of triangle PQR at origin A = Area of triangle PQR at origin C.
The area is the same in both cases because the triangle remains the same no matter which point is considered as the origin.
6. The vertices of a ∆ ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E, respectively, such that AD/AB = AE/AC = 1/4. Calculate the area of the ∆ ADE and compare it with the area of ∆ ABC. (Recall Theorem 6.2 and Theorem 6.6)
Solution –
Given: The vertices of a ∆ ABC are A (4, 6), B (1, 5) and C (7, 2)

AD/AB = AE/AC = 1/4
AD/(AD + BD) = AE/(AE + EC) = 1/4
Point D and Point E divide AB and AC, respectively, in ratio 1:3.
Coordinates of D can be calculated as follows:
x = (m1x2 + m2x1)/(m1 + m2) and y = (m1y2 + m2y1)/(m1 + m2)
Here, m1 = 1 and m2 = 3
Consider line segment AB which is divided by point D at the ratio 1:3.
x = [3(4) + 1(1)]/4 = 13/4
y = [3(6) + 1(5)]/4 = 23/4
Similarly, the coordinates of E can be calculated as follows:
x = [1(7) + 3(4)]/4 = 19/4
y = [1(2) + 3(6)]/4 = 20/4 = 5
Find the area of triangle:
Using formula: Area of a triangle = 1/2 × [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
The area of triangle ∆ ABC can be calculated as follows:
= ½ [4(5 – 2) + 1( 2 – 6) + 7( 6 – 5)]
= ½ (12 – 4 + 7) = 15/2 sq unit
The area of ∆ ADE can be calculated as follows:
= ½ [4(23/4 – 5) + 13/4 (5 – 6) + 19/4 (6 – 23/4)]
= ½ (3 – 13/4 + 19/16)
= ½ ( 15/16 ) = 15/32 sq unit
Hence, the ratio of the area of triangle ADE to the area of triangle ABC = 1 : 16.
7. Let A (4, 2), B (6, 5), and C (1, 4) be the vertices of ∆ ABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP:PD = 2:1.
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively, such that BQ:QE = 2:1 and CR:RF = 2 : 1.
(iv) What do you observe?
[Note: The point which is common to all the three medians is called the centroid, and this point divides each median in the ratio 2:1.]
(v) If A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of triangle ABC, find the coordinates of the centroid of the triangle.
Solution –
(i) Coordinates of D can be calculated as follows:
Coordinates of D = ( (6+1)/2, (5+4)/2 ) = (7/2, 9/2)
So, D is (7/2, 9/2)
(ii) Coordinates of P can be calculated as follows:
Coordinates of P = ( [2(7/2) + 1(4)]/(2 + 1), [2(9/2) + 1(2)]/(2 + 1))
= (11/3, 11/3)
So, P is (11/3, 11/3)
(iii) Coordinates of E can be calculated as follows:
Coordinates of E = ( (4+1)/2, (2+4)/2 ) = (5/2, 6/2)
= (5/2, 3)
So, E is (5/2, 3)
Points Q and P would be coincident because the medians of a triangle intersect each other at a common point called the centroid. Coordinate of Q can be given as follows:
Coordinates of Q =( [2(5/2) + 1(6)]/(2 + 1), [2(3) + 1(5)]/(2 + 1) )
= (11/3, 11/3)
F is the midpoint of the side AB
Coordinates of F = ((4+6)/2, (2+5)/2 )
= (5, 7/2)
Point R divides the side CF in ratio 2 : 1
Coordinates of R = ( [2(5) + 1(1)]/(2 + 1), [2(7/2) + 1(4)]/(2 + 1) )
= (11/3, 11/3)
(iv) Coordinates of P, Q and R are the same, which shows that medians intersect each other at a common point, i.e. centroid of the triangle.
(v) If A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of triangle ABC, the coordinates of the centroid can be given as follows:
x = (x1 + x2 + x3)/3 and y = (y1 + y2 + y3)/3
8. ABCD is a rectangle formed by the points A (-1, – 1), B (-1, 4), C (5, 4) and D (5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA, respectively. Is the quadrilateral PQRS a square, a rectangle or a rhombus? Justify your answer.
Solution –
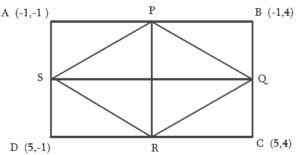
P id the midpoint of side AB,
Coordinate of P = ( (-1 – 1)/2, (-1 + 4)/2 ) = (-1, 3/2)
Similarly, Q, R and S are (As Q is the midpoint of BC, R is the midpoint of CD and S is the midpoint of AD)
Coordinate of Q = (2, 4)
Coordinate of R = (5, 3/2)
Coordinate of S = (2, -1)
Now,
Length of PQ = √[(-1 – 2)2 + (3/2 – 4)2] = √(61/4) = √61/2
Length of SP = √[(2 + 1)2 + (-1 – 3/2)2] = √(61/4) = √61/2
Length of QR = √[(2 – 5)2 + (4 – 3/2)2] = √(61/4) = √61/2
Length of RS = √[(5 – 2)2 + (3/2 + 1)2] = √(61/4) = √61/2
Length of PR (diagonal) = √[(-1 – 5)2 + (3/2 – 3/2)2] = 6
Length of QS (diagonal) = √[(2 – 2)2 + (4 + 1)2] = 5
The above values show that PQ = SP = QR = RS = √61/2, i.e. all sides are equal.
But PR ≠ QS, i.e. diagonals are not of equal measure.
Hence, the given figure is a rhombus.

Leave a Reply