NCERT Solutions Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1

NCERT Solutions Class 10 Maths 
Chapter – 7 (Coordinate Geometry) 

The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 7 Coordinate Geometry Exercise 7.1 has been provided here to help the students in solving the questions from this exercise. 

Chapter : 7 Coordinate Geometry

Exercise – 7.1

1. Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (- a, – b)

Solution – Distance formula to find the distance between two points (x1, y1) and (x2, y2) is, say d,
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

(i) Distance between (2, 3) and (4, 1) is given by
d = \sqrt{(4 - 2)^2 + (1 - 3)^2}
d = \sqrt{(2)^2 + (- 2)^2}
d = \sqrt{8}
d = 2\sqrt{2}

(ii) Distance between (−5, 7) and (−1, 3) is given by

d = \sqrt{(-1 + 5)^2 + (3 - 7)^2}
d = \sqrt{(4)^2 + (- 4)^2}
d = \sqrt{32}
d = 4\sqrt{2}

(iii) Distance between (a, b) and (− a, − b) is given by
d = \sqrt{(a -(-a))^2 + (b - (-b))^2}
d = \sqrt{(2a)^2 + (2b)^2}
d = \sqrt{4a^2 +4b^2}
d = 2\sqrt{a^2+b^2}

2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns, A and B, discussed in Section 7.2?

Solution – Distance between points (0, 0) and (36, 15)
= \sqrt{(36-0)^2 + (15-0)^2}
= \sqrt{1296 + 225}
= \sqrt{1521}
= 39
Yes, Assume town A at origin point (0, 0).
Therefore, town B will be at point (36, 15) with respect to town A.
And hence, as calculated above, the distance between town A and B will be 39 km.

3. Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution –  Let the points (1, 5), (2, 3), and (- 2,-11) be representing the vertices A, B, and C of the given triangle respectively.
Let A = (1, 5), B = (2, 3) and C = (- 2,-11)
Find the distance between points: say AB, BC and CA
∴ AB = \sqrt{(2-1)^2 + (3-5)^2}
= \sqrt{(1)^2 + (-2)^2}
= \sqrt{1+4}
= \sqrt{5}

BC = \sqrt{(-2-2)^2 + (-11-3)^2}
= \sqrt{(-4)^2 + (-14)^2}
= \sqrt{16 + 196}
= \sqrt{212} 

CA = \sqrt{(-2-1)^2 + (-11-5)^2}
= \sqrt{(-3)^2 + (-16)^2}
= \sqrt{9+256}
= \sqrt{265}

Since AB + BC ≠ CA
Therefore, the points (1, 5), (2, 3), and (- 2, – 11) are not collinear.

4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Solution – Let the points (5, – 2), (6, 4), and (7, – 2) are representing the vertices A, B, and C of the given triangle respectively.
AB = \sqrt{(6-5)^2 + (4+2)^2}
= \sqrt{(-1)^2 + (6)^2}
= \sqrt{37}

BC = \sqrt{(7-6)^2 + (-2-4)^2}
= \sqrt{(-1)^2 + (6)^2}
= \sqrt{37}

CA = \sqrt{(7-5)^2 + (-2+2)^2}
= \sqrt{4}
= 2
Therefore, AB = BC
As two sides are equal in length, therefore, ABC is an isosceles triangle.

5. In a classroom, 4 friends are seated at points A, B, C and D, as shown in Fig. 7.8. Champa and Chameli walk into the class, and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using the distance formula, find which of them is correct.
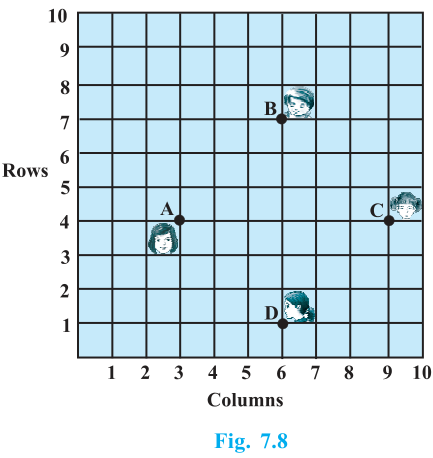
NCERT Class 10 Maths Solution

Solution – From the figure, the coordinates of points A, B, C and D are (3, 4), (6, 7), (9, 4) and (6,1).
Find the distance between points using the distance formula, we get
AB = \sqrt{(6-3)^2 + (7-4)^2}
= \sqrt{3^2 + 3^2}
= \sqrt{18}
= 3\sqrt{2}

BC = \sqrt{(9-6)^2 + (4-7)^2}
= \sqrt{3^2 +(-3)^2}
= \sqrt{18}
= 3\sqrt{2}

CD = \sqrt{(6-9)^2 +(1-4)^2}
= \sqrt{(-3)^2+(-3)^2}
= \sqrt{18}
= 3\sqrt{2}

DA = \sqrt{(6-3)^2 +(1-4)^2}
= \sqrt{3^2 +(-3)^2}
= \sqrt{18}
= 3\sqrt{2}

Diagonal AC = \sqrt{(3-9)^2 + (4-4)^2}
= \sqrt{(-6)}^2 
= 6

Diagonal BD = \sqrt{(6-6)^2 + (7-1)^2}
= \sqrt{(6)}^2
= 6
It can be observed that all sides of this quadrilateral ABCD are of the same length and also the diagonals are of the same length.
Therefore, ABCD is a square and hence, Champa was correct

6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0)
(ii) (- 3, 5), (3, 1), (0, 3), (- 1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)

Solution –
(i) Let the points (- 1, – 2), (1, 0), ( – 1, 2), and ( – 3, 0) represent the vertices A, B, C, and D of the given quadrilateral, respectively.
AB = \sqrt{(1+1)^2 +(0+2)^2}
= \sqrt{4+4}
= 2\sqrt{2}

BC = \sqrt{(-1-1)^2 + (2-0)^2}
= = \sqrt{4+4}
= 2\sqrt{2}

CD = \sqrt{(-3+1)^2 + (0-2)^2}
= \sqrt{4+4}
= 2\sqrt{2}

DA = \sqrt{(-3+1)^2 + (0-2)^2}
= \sqrt{4+4}
= 2\sqrt{2}

Diagonal AC = \sqrt{(-1+1)^2 +(2+2)^2}
= \sqrt{0 +16}
= 4

Diagonal BD = \sqrt{(-3-1)^2 +(0-0)^2}
= \sqrt{16+0}
= 4
Side length = AB = BC = CD = DA = 2√2
Diagonal Measure = AC = BD = 4
Therefore, the given points are the vertices of a square.

(ii) Let the points (- 3, 5), (3, 1), (0, 3), and (- 1, – 4) represent the vertices A, B, C, and D of the given quadrilateral, respectively.
AB = \sqrt{(-3-3)^2 +(1-5)^2}
= \sqrt{36 + 16}
= 2\sqrt{13}

BC = \sqrt{(0-3)^2 +(3-1)^2}
= \sqrt{9 +4} 
= \sqrt{13}

CD = \sqrt{(-1-0)^2 +(-4-3)^2}
= \sqrt{1+49}
= 5\sqrt{2}

AD = \sqrt{(-1+3)^2 +(-4-5)^2}
= \sqrt{4+81}
= \sqrt{85}

It’s also seen that points A, B and C are collinear.
So, the given points can only form 3 sides, i.e. a triangle and not a quadrilateral which has 4 sides.
Therefore, the given points cannot form a general quadrilateral.

(iii) Let the points (4, 5), (7, 6), (4, 3), and (1, 2) represent the vertices A, B, C, and D of the given quadrilateral, respectively.

AB = \sqrt{(7-4)^2 +(6-5)^2}
= \sqrt{9+1}
= \sqrt{10}

BC = \sqrt{(4-7)^2 +(3-6)^2}
= \sqrt{9+9}
= 3\sqrt{2}

CD = \sqrt{(1-4)^2 +(2-3)^2}
= \sqrt{9+1}
= \sqrt{10}

AD = \sqrt{(1-4)^2 +(2-5)^2}
= \sqrt{9+9}
= 3\sqrt{2}

Diagonal AC = \sqrt{(4-4)^2 +(3-5)^2}
= \sqrt{0 +4}
= 2

Diagonal BD = \sqrt{(1-7)^2 +(2-6)^2}
= \sqrt{36+16}
= 2\sqrt{13}

Opposite sides of this quadrilateral are of the same length. However, the diagonals are of different lengths. Therefore, the given points are the vertices of a parallelogram.

7. Find the point on the x-axis which is equidistant from (2, – 5) and (- 2, 9).
Solution – To find a point on the X-axis.
Therefore, its Y-coordinate will be 0. Let the point on the x-axis be (x,0).
Consider A = (x, 0); B = (2, – 5) and C = (- 2, 9).
AB = \sqrt{(2-x)^2 + (-5-0)^2}
= \sqrt{(2-x)^2 +25}

AC = \sqrt{(-2-x)^2 + (9-0)^2}
= \sqrt{(-2-x)^2 + 81}

Since both the distance are equal in measure, so AB = AC 
\sqrt{(2-x)^2 +25} = \sqrt{(-2-x)^2 + 81}

(2 – x)2 + 25 = [-(2 + x)]2 + 81
(2 – x)2 + 25 = (2 + x)2 + 81
x2 + 4 – 4x + 25 = x2 + 4 + 4x + 81
8x = 25 – 81 = -56
x = -7
Therefore, the point is (- 7, 0).

8. Find the values of y for which the distance between the points P (2, – 3) and Q (10, y) is 10 units.
Solution –
Given : Distance between (2, – 3) and (10, y) is 10.
Using the distance formula,
PQ = \sqrt{(10-2)^2 +(y+3)^2}
= \sqrt{8^2 +(y+3)^2}
Since PQ = 10 
\sqrt{8^2 +(y+3)^2} = 10
64 + (y + 3)2 = 100
(y + 3)2 = 36
y + 3 = ±6
y + 3 = +6 or y + 3 = −6
y = 6 – 3 = 3
or
y = – 6 – 3 = -9
Therefore, y = 3 or -9.

9. If Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), find the values of x. Also, find the distance QR and PR.
Solution –
Given : Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), which means PQ = QR

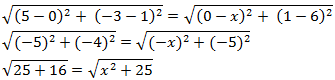
Squaring both sides to omit square root
41 = x2 + 25
x2 = 16
x = ± 4
x = 4 or x = -4
Coordinates of Point R will be R (4, 6) or R (-4, 6),
If R (4, 6), then QR

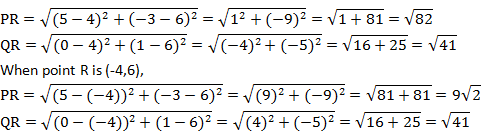
10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (- 3, 4).
Solution – Point (x, y) is equidistant from (3, 6) and (- 3, 4).

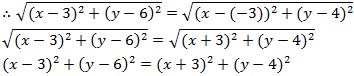
Squaring both sides,
(x – 3)2 + (y – 6)2 = (x + 3)2 +(y – 4)2
x2 + 9 – 6x + y2+ 36 – 12y = x2 + 9 + 6x + y2 +16 – 8y
36 – 16 = 6x + 6x + 12y – 8y
20 = 12x + 4y
3x + y = 5
3x + y – 5 = 0

Go Back To Chapters

 

You might be interested in

Admin

Leave a Reply

Your email address will not be published.

Latest from Class 10 Maths