NCERT Solutions Class 10 Maths
Chapter – 14 (Statistics)
The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 14 Statistics Exercise 14.4 has been provided here to help the students in solving the questions from this exercise.
Chapter : 14 Statistics
- NCERT Class 10 Maths Solution Ex – 14.1
- NCERT Class 10 Maths Solution Ex – 14.2
- NCERT Class 10 Maths Solution Ex – 14.3
Exercise – 14.4
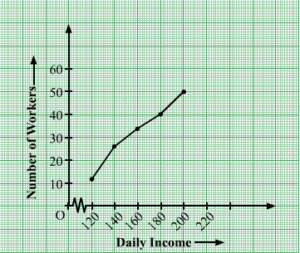
1. The following distribution gives the daily income of 50 workers in a factory.
| Daily income (in Rs.) | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive.
Solution – Convert the given distribution table to a less than type cumulative frequency distribution, and we get
| Daily Income | Cumulative Frequency (or) Number of workers |
| Less than 120 | 12 |
| Less than 140 | 26 |
| Less than 160 | 34 |
| Less than 180 | 40 |
| Less than 200 | 50 |
From the table plot the points corresponding to the ordered pairs such as (120, 12), (140, 26), (160, 34), (180, 40) and (200, 50) on graph paper and the plotted points are joined to get a smooth curve and the obtained curve is known as less than type ogive curve
2. During the medical check-up of 35 students of a class, their weights were recorded as follows:
| Weight in kg | Number of students |
| Less than 38 | 0 |
| Less than 40 | 3 |
| Less than 42 | 5 |
| Less than 44 | 9 |
| Less than 46 | 14 |
| Less than 48 | 28 |
| Less than 50 | 32 |
| Less than 52 | 35 |
Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula.
Solution – From the given data, to represent the table in the form of graph, choose the upper limits of the class intervals are in x-axis and frequencies on y-axis by choosing the convenient scale. Now plot the points corresponding to the ordered pairs given by (38, 0), (40, 3), (42, 5), (44, 9),(46, 14), (48, 28), (50, 32) and (52, 35) on a graph paper and join them to get a smooth curve. The curve obtained is known as less than type ogive.
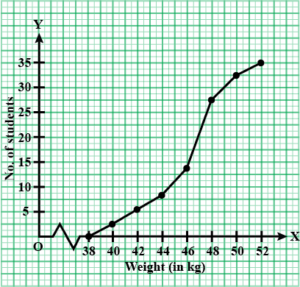
Locate the point 17.5 on the y-axis and draw a line parallel to the x-axis cutting the curve at a point. From the point, draw a perpendicular line to the x-axis. The intersection point perpendicular to x-axis is the median of the given data. Now, to find the median by making a table.
| Class interval | Number of students(Frequency) | Cumulative Frequency | |
| Less than 38 | 0 – 38 | 0 | 0 |
| Less than 40 | 38 – 40 | 3 – 0 = 3 | 3 |
| Less than 42 | 40 – 42 | 5 – 3 = 2 | 5 |
| Less than 44 | 42 – 44 | 9 – 5 = 4 | 9 |
| Less than 46 | 44 – 46 | 14 – 9 = 5 | 14 |
| Less than 48 | 46 – 48 | 28 – 14 = 14 | 28 |
| Less than 50 | 48 – 50 | 32 – 28 = 4 | 32 |
| Less than 52 | 50 – 52 | 35 – 22 = 3 | 35 |
Here, N = 35 and N/2 = 35/2 = 17.5
Median class = 46 – 48
l = 46,
h = 2,
cf = 14,
f = 14
The mode formula is given as:
Median =
= 46 + [(17.5 – 14)/ 14] × 2
= 46 + 0.5
= 46 + 0.5 = 46.5
Thus, median is verified.
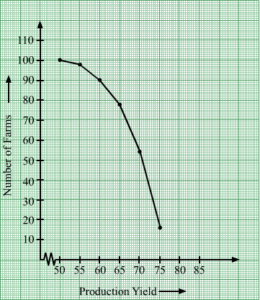
3. The following table gives production yield per hectare of wheat of 100 farms of a village.
| Production Yield (in kg/ha) | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 |
| Number of Farms | 2 | 8 | 12 | 24 | 38 | 16 |
Change the distribution to a more than type distribution and draw its ogive.
Solution – Converting the given distribution to a more than type distribution, we get
| Production Yield (kg/ha) | Number of farms |
| More than or equal to 50 | 100 |
| More than or equal to 55 | 100 – 2 = 98 |
| More than or equal to 60 | 98 – 8 = 90 |
| More than or equal to 65 | 90 – 12 = 78 |
| More than or equal to 70 | 78 – 24 = 54 |
| More than or equal to 75 | 54 – 38 = 16 |
From the table obtained draw the ogive by plotting the corresponding points where the upper limits in x-axis and the frequencies obtained in the y-axis are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on the graph paper. The graph obtained is known as more than type ogive curve.

Leave a Reply