NCERT Solutions Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4

Exercise – 9.4

1. Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Answer – Given: The parallelogram and the rectangle have the same base and equal areas, therefore, they will also lie between the same parallels.
Consider the parallelogram ABCD and rectangle ABEF as follows.

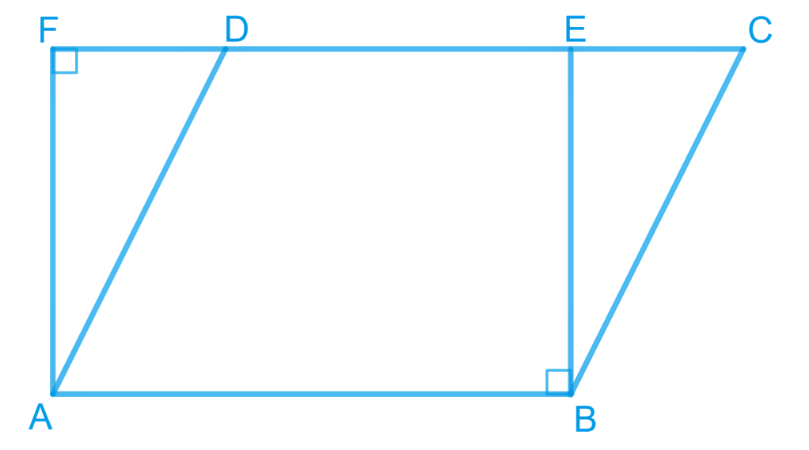
Here, it can be observed that parallelogram ABCD and rectangle ABEF are lying between the same parallels AB and CF.
It is given that the opposite sides of a parallelogram and a rectangle are of equal lengths.
Therefore, AB = EF (Opposite sides of a rectangle are equal.)
AB = CD (Opposite sides of a parallelogram are equal.)
∴ CD = EF
∴ AB + CD = AB + EF                   —————-(i)
Now, in a right-angled triangle AFD, AD is a hypotenuse.
∴ AF < AD                                       —————-(ii)
Similarly, in a right angled triangle EBC, EB is altitude and BC is a hypotenuse

∴ BE < BC                                       —————-(iii)
Adding equation (ii) and (iii),
∴ AF + BE < AD + BC                  —————-(iv)
Now, from equations (i) and (iv), we obtain
AB + EF + AF + BE < AD + BC + AB + CD
Perimeter of rectangle ABEF < Perimeter of parallelogram ABCD.

2. In Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?

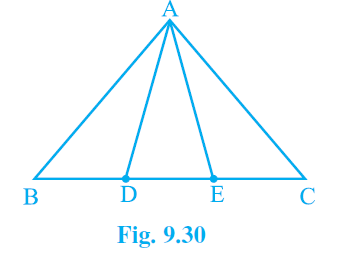
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide DABC into n triangles of equal areas.]

Answer – Given : BD = DE = EC
To prove : Area (△ABD) = Area (△ADE) = Area (△AEC)
Proof,
In (△ABE), AD is median [since, BD = DE, given]
We know that, the median of a triangle divides it into two parts of equal areas
Area (△ABD) = Area (△AED)         ————-—(i)
Similarly,
In (△ADC), AE is median [since, DE = EC, given]
Area (ADE) = Area (AEC)                 ———–—(ii)
From the equation (i) and (ii), we get
Area (ABD) = Area (ADE) = Area (AEC)

3. In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

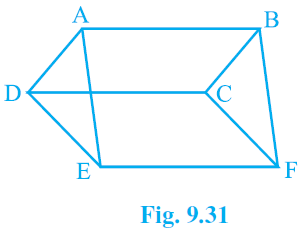
Answer – Given : ABCD, DCFE and ABFE are parallelograms
To prove : ar (△ADE) = ar (△BCF)
In △ADE and △BCF,
AD = BC [Since they are the opposite sides of the parallelogram ABCD]
DE = CF [Since they are the opposite sides of the parallelogram DCFE]
AE = BF [Since they are the opposite sides of the parallelogram ABFE]
△ADE ≅ △BCF [Using SSS Congruence theorem]
Area (△ADE) = Area (△BCF)       [By CPCT]

4. In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

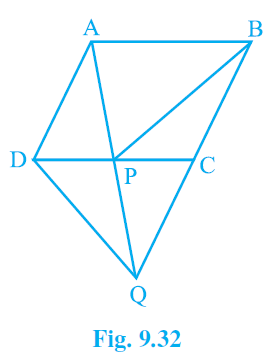
[Hint : Join AC.]

Answer – Given: ABCD is a parallelogram
AD = CQ
To prove: Area (△BPC) = Area (△DPQ)
In △ADP and △QCP,
∠APD = ∠QPC [Vertically Opposite Angles]
∠ADP = ∠QCP [Alternate Angles]
AD = CQ [given]
△ABO ≅ △ACD [AAS congruency]
DP = CP [CPCT]
In △CDQ, QP is median. [Since, DP = CP]
Since, median of a triangle divides it into two parts of equal areas.
Area (△DPQ) = Area (△QPC)             —————(i)
In △PBQ, PC is median. [Since, AD = CQ and AD = BC ⇒ BC = QC]
Since, median of a triangle divides it into two parts of equal areas.
Area (△QPC) = Area (△BPC)                        —————(ii)
From the equation (i) and (ii), we get
Area (△BPC) = Area (△DPQ)

5. In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:

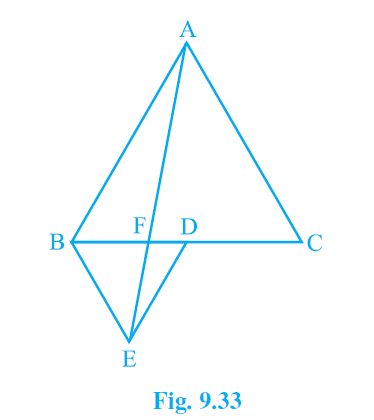
(i) ar (BDE) =1/4 ar (ABC)
(ii) ar (BDE) = ½ ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)

Answer –
(i) ar (BDE) =1/4 ar (ABC)
Let G and H be the mid-points of side AB and AC.

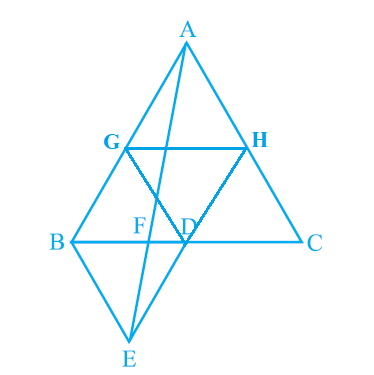
Line segment GH is joining the mid-points and is parallel to the third side. Therefore, GH will be half of the length of BC (mid-point theorem).
∴ GH = 1/2 BC and GH || BD
∴ GH = BD = DC and GH || BD (D is the mid-point of BC)
Similarly,
GD = HC = HA
HD = AG = BG
Therefore, clearly, triangle ABC is divided into 4 equal equilateral triangles viz ΔBGD, ΔAGH, ΔDHC, and ΔGHD.
In other words,
ΔBGD = 1/4 ΔABC
Now consider ΔBDG and ΔBDE
BD = BD (Common base)
As both triangles are equilateral triangle, we can say BG = BE
DG = DE
Therefore,
ΔBDG ≅ ΔBDE [By SSS congruency]
The SSS rule states that: If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
Thus, area (ΔBDG) = area (ΔBDE)
ar (ΔBDE) = 1/4 ar (ΔABC)
Hence proved.

(ii) ar (BDE) = ½ ar (BAE)
Join points A and D.

Area (ΔBDE) = Area (ΔAED) (Common base DE and DE || AB)
Area (ΔBDE) – Area (ΔFED) = Area (ΔAED) – Area (ΔFED)
Now Area (ΔBEF) = Area (ΔAFD)                —————–(1)
Area (ΔABD) = Area (ΔABF) + Area (ΔAFD)
Area (ΔABD) = Area (ΔABF) + Area (ΔBEF) [From equation (1)]
Area (ΔABD) = Area (ΔABE)                        ——————(2)
AD is the median in ΔABC (D is the midpoint of BC)
ar (ΔABD) = 1/2 ar (ΔABC) 
ar (ΔBDE) = 1/4 ar (ΔABC) [As proved earlier in (i)]
ar(ΔABD) = 2 ar (ΔBDE)                             ——————(3)
From (2) and (3), we obtain,
2 Area (ΔBDE) = Area (ΔABE)
Area (BDE) = 1/2 Area (BAE)

(iii) ar (ABC) = 2 ar (BEC)
Join points C and E

Area (ΔABE) = Area (ΔBEC) (Common base BE and BE || AC)
Area (ΔABF) + Area (ΔBEF) = Area (ΔBEC)
Using equation (1), we obtain,
Area (ΔABF) + Area (ΔAFD) = Area (ΔBEC)
Area (ΔABD) = Area (ΔBEC)
1/2 Area (ΔABC) = Area (ΔBEC)
Area(ΔABC) = 2 Area (ΔBEC)

(iv) ar (BFE) = ar (AFD)
ΔBDE and ΔAED lie on the same base (DE) and between the parallels DE and AB.
Area (ΔBDE) = Area (ΔAED)
Area (ΔBDE) – Area (ΔFED) = Area (ΔAED) – Area (ΔFED) [Subtracting ar (ΔFED) on both the sides]
Area (ΔBFE) = Area (ΔAFD)

(v) ar (BFE) = 2 ar (FED)
Let h be the height of vertex E, corresponding to the side BD in ΔBDE
Let H be the height of vertex A, corresponding to the side BC in ΔABC.
Area (ABC) = 1/2 × BC × H
Area (BDE) = 1/2 × 1/2(BC) × h
In (i), it was shown that ar (BDE) = 1/4 Area (ABC)
Therefore, H = 2h
Now,
Area (AFD) = 1/2 × FD × 2h
Area (FED) = 1/2 × (FD) × h
Hence, Area (AFD) = 2 × Area (FED)
In (iv), it was shown that Area (ΔBFE) = Area (ΔAFD)
Therefore, Area (ΔBFE) = Area (ΔAFD) = 2 Area (ΔFED)
Hence proved.

(vi) ar (FED) = 1/8 ar (AFC)
Area (ΔAFC) = Area (ΔAFD) + Area (ΔADC)
= 2 Area (ΔFED) + 1/2 Area (ΔABC) [using (v)]
= 2 Area (ΔFED) + 1/2 [4 × Area (ΔBDE)] [Using result of part (i)]
= 2 Area (ΔFED) + 2 Area (ΔBDE)
= 2 Area (ΔFED) + 2 Area (ΔAED)
[ΔBDE and ΔAED are on the same base and between same parallels]
= 2 Area (ΔFED) + 2 [Area (ΔAFD) + Area (ΔFED)]
= 2 Area (ΔFED) + 2 Area (ΔAFD) + 2 Area (ΔFED) 
= 4 Area (ΔFED) + 4 Area (ΔFED) [using result of (v)]
⇒ Area (ΔAFC) = 8 Area (ΔFED)
⇒ Area (ΔFED) = 1/8 Area (ΔAFC)

6. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that
ar (APB)×ar (CPD) = ar (APD)×ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]

Answer – Given: The diagonal AC and BD of the quadrilateral ABCD, intersect each other at point E.
Construction: From A, draw AM perpendicular to BD
From C, draw CN perpendicular to BD

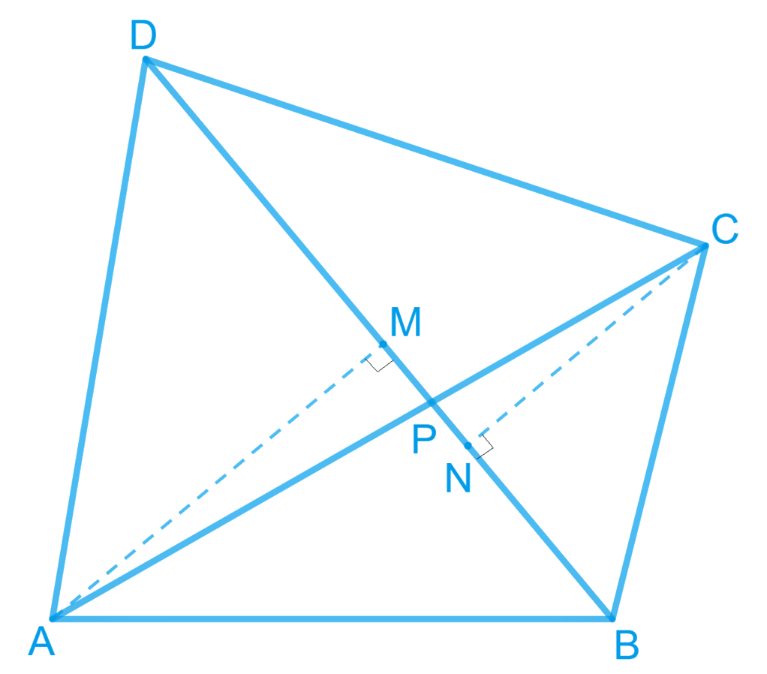
To Prove : Area (ΔAED) Area (ΔBEC) = Area (ΔABE) × Area (ΔCDE)
Area (ΔABE) = ½ × BE × AM                 ——————(i)
Area (ΔAED) = ½ × DE × AM                ——————(ii)
Dividing eq. (ii) by (i) , we get,

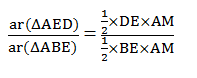
Area (AED)/Area (ABE) = DE/BE         —————–(iii)
Similarly,
Area (CDE)/Area (BEC) = DE/BE        —————— (iv)
From eq. (iii) and (iv) , we get
Area (AED)/Area (ABE) = Area (CDE)/Area (BEC)
Area (ΔAED) × Area (ΔBEC) = Area (ΔABE) × Area (ΔCDE)
Hence proved.

7. P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that:
(i) ar (PRQ) = ½ ar (ARC)
(ii) ar (RQC) = (3/8) ar (ABC)
(iii) ar (PBQ) = ar (ARC)

Answer – Let’s draw the given triangle ABC.

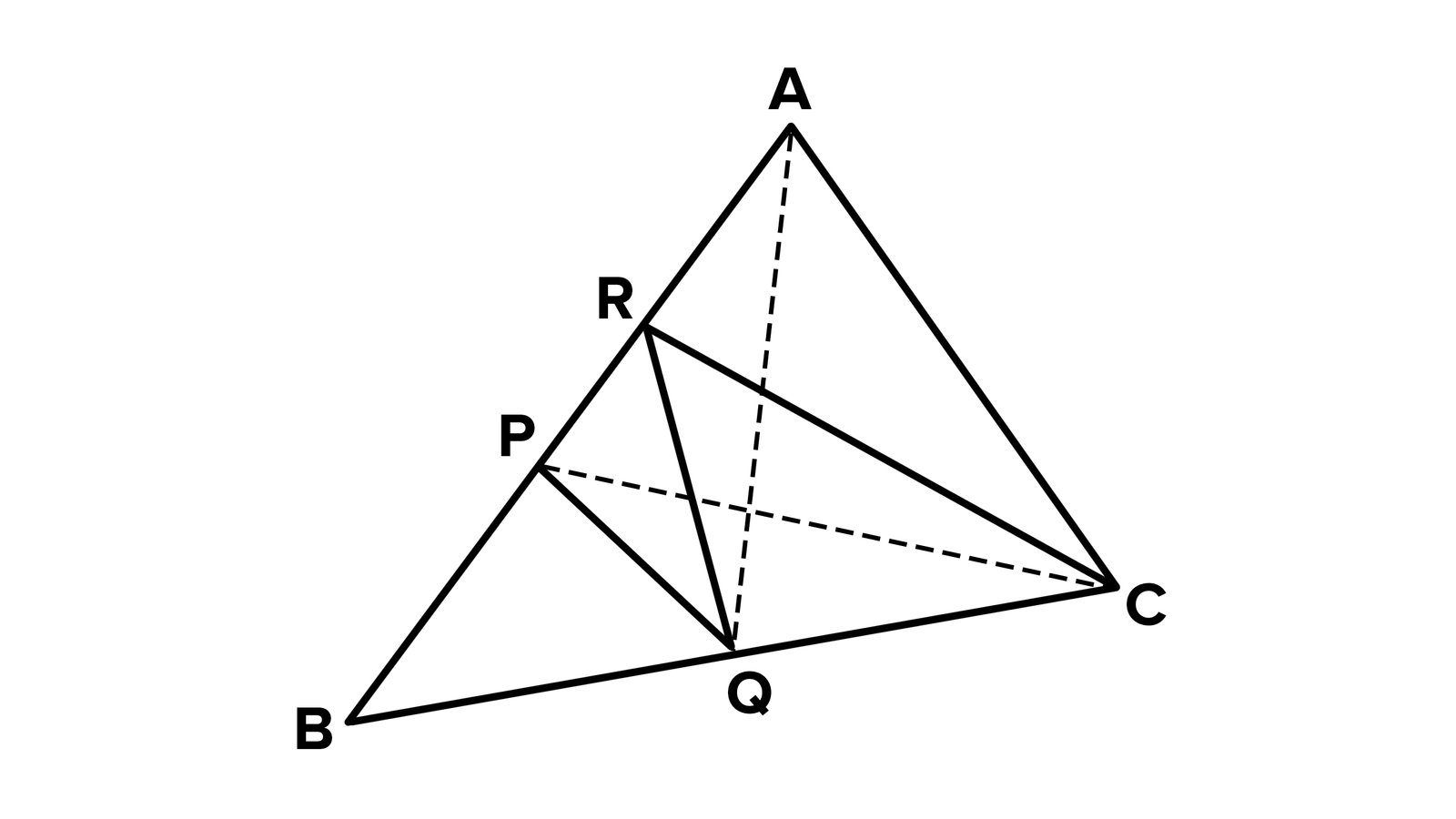
(i) ar (PRQ) = ½ ar (ARC)
PC is the median of ΔABC.
∴ Area (ΔBPC) = Area (ΔAPC)       ————- (i)
RC is the median of ΔAPC.
∴ Area (ΔARC) = 1/2 Area (ΔAPC) —————- (ii)
[Median divides the triangle into two triangles of equal area]
PQ is the median of ΔBPC.
∴ Area (ΔPQC) = 1/2 Area (ΔBPC)  —————- (iii)
From equation (i) and (iii), we get,
Area (ΔPQC) = 1/2 Area (ΔAPC)     ——————- (iv)
From equation (ii) and (iv), we get,
Area (ΔPQC) = Area (ΔARC)            ——————— (v)
We are given that P and Q are the mid-points of AB and BC, respectively.
∴ PQ || AC and PQ = 1/2 AC
⇒ Area (ΔAPQ) = Area (ΔPQC)          —————— (vi) [triangles between same parallel are equal in area ]
From equation (v) and (vi), we get
Area (ΔAPQ) = Area (ΔARC)              —————— (vii)
R is the mid-point of AP. Therefore, RQ is the median of ΔAPQ.
∴ Area (ΔPRQ) = 1/2 Area (ΔAPQ)    ———————– (viii)
From (vii) and (viii), we get,
∴ Area (ΔPRQ) = 1/2 Area (ΔARC)

(ii) ar (RQC) = (3/8) ar (ABC)
PQ is the median of ΔBPC.
∴ Area (ΔPQC) = 1/2 Area (ΔBPC) = 1/2 × 1/2 Area (ΔABC)       ——————- (ix)
Also,
Area (ΔPRC) = 1/2 Area (ΔAPC) [Using (iv)]
Area (ΔPRC) = 1/2 × 1/2 Area (ΔABC) = 1/4 Area (ΔABC)          ——————- (x)
Adding equation (ix) and (x), we get,
Area (ΔPQC) + Area (ΔPRC) = ( 1/4 + 1/4 ) Area (ΔABC)
⇒ Area (quadrilateral PQCR) = 1/2 Area (ΔABC)                  ——————— (xi)
Subtracting ar (ΔPRQ) from the both sides,
Area (quadrilateral PQCR) – Area (ΔPRQ) = 1/2 Area (ΔABC) – Area (ΔPRQ)
⇒ Area (ΔRQC) = 1/2 Area (ΔABC) – 1/2 Area (ΔARC) [Using result (i)]
⇒ Area (ΔRQC) = 1/2 Area (ΔABC) – 1/2 × 1/2 Area (ΔAPC)
⇒ Area (ΔRQC) = 1/2 Area (ΔABC) – 1/4 Area (ΔAPC)
⇒ Area (ΔRQC) = 1/2 Area (ΔABC) – 1/4 × 1/2 Area (ΔABC) [PC is median of DABC]
⇒ Area (ΔRQC) = 1/2 Area (ΔABC) – 1/8 Area (ΔABC)
⇒ Area (ΔRQC) = (1/2 – 1/8) × Area (ΔABC)
⇒ Area (ΔRQC) = 3/8 × Area (ΔABC)

(iii) ar (PBQ) = ar (ARC)
Area (ΔPRQ) = 1/2 Area (ΔARC) [Using result (i)]
⇒ 2 Area (ΔPRQ) = Area (ΔARC)          ——————- (xii)
Area (ΔPRQ) = 1/2 Area (ΔAPQ) [RQ is the medium of ΔAPQ]           ————- (xiii)
But Area (ΔAPQ) = Area (ΔPQC) [Using reason of eq. (vi)]               ————— (xiv)
From eq. (xiii) and (xiv), we get,
Area (ΔPRQ) = 1/2 Area (ΔPRQ)            —————- (xv)
But,
Area (ΔBPQ) = Area (ΔPQC) [PQ is the median of DBPC]  ————– (xvi)
From eq. (xv) and (xvi), we get,
Area (ΔPRQ) = 1/2 Area (ΔBPQ)              —————–  (xvii)
Now from (xii) and (xvii), we get,
2 × 1/2 Area (ΔBPQ) = Area (ARC)
⇒ Area (ΔBPQ) = Area (ΔARC)

8. In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB, respectively. Line segment AX ^ DE meets BC at Y. Show that:

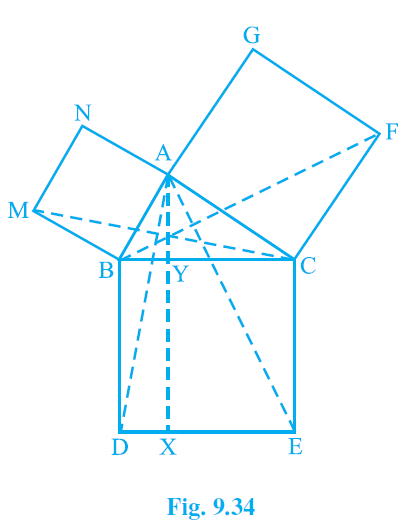
(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2ar(MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2ar(FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN)+ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.

Answer – We can use a suitable congruency rule to show the triangles congruent. Also, we can use some theorem or properties like triangle and parallelogram on the same base and between the same parallels. The Triangle area will be half of the parallelogram area.

(i) ΔMBC ≅ ΔABD
We know that each angle of a square is 90°.
Hence,
∠ABM = ∠DBC = 90^o
∴ ∠ABM + ∠ABC = ∠DBC + ∠ABC
∴ ∠MBC = ∠ABD
In ΔMBC and ΔABD,
∠MBC = ∠ABD (Proved above)
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∴ ΔMBC ≅ ΔABD (By SAS congruence rule)

(ii) ar(BYXD) = 2ar(MBC)
We have ΔMBC ≅ ΔABD
∴ ar (ΔMBC) = ar (ΔABD)         ————-(1)
It is given that AX ⊥ DE and BD ⊥ DE (Adjacent sides of square BDEC)
∴ BD|| AX (Two lines perpendicular to the same line are parallel to each other)
∆ABD and parallelogram BYXD are on the same base BD and between the same parallels BD and AX.
Area (∆BYXD) = 2 Area (∆MBC) [Using equation (1)]  —————- (2)

(iii) ar(BYXD) = ar(ABMN)
ΔMBC and parallelogram ABMN lie on the same base MB and between the same parallels MB and NC.
2 Area (ΔMBC) = Area (ABMN)
Area (BYXD) = Area (ABMN) [Using equation (2)]            —————- (3)

(iv) ΔFCB ≅ ΔACE
We know that each angle of a square is 90°.
∴ ∠FCA = ∠BCE = 90^o
∴ ∠FCA + ∠ACB = ∠BCE + ∠ACB
Adding ∠ACB on both the sides
∴ ∠FCB = ∠ACE
In ΔFCB and ΔACE,
FC = AC (Sides of square ACFG)
CB = CE (Sides of square BCED)
ΔFCB ≅ ΔACE (SAS congruence rule)
SAS Congruence Rule – If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.

(v) ar(CYXE) = 2ar(FCB)
It is given that AX ^ DE and CE ^ DE (Adjacent sides of square BDEC)
Hence, CE || AX (Two lines perpendicular to the same line are parallel to each other) Consider ∆ACE and parallelogram CYXE
DACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
∴ Area (ΔCYXE) = 2 Area (ΔACE)         —————— (4)
We had proved that
ΔFCB ≅ ΔACE
Area (ΔFCB) ≅ Area (ΔACE)                  —————– (5)
On comparing equations (4) and (5), we obtain
Area (CYXE) = 2 Area (ΔFCB)       —————– (6)

(vi) ar(CYXE) = ar(ACFG)
Consider ∆FCB and parallelogram ACFG
ΔFCBand parallelogram ACFG are lying on the same base CF and between the same parallels CF and BG.
∴ Area (ACFG) = 2 Area (ΔFCB)
∴ Area (ACFG) = Area (CYXE) [Using equation (6)]           ——————– (7)

(vii) ar(BCED) = ar(ABMN)+ar(ACFG)
From the figure, it is evident that
Area (BCED) = Area (BYXD) + Area (CYXE)
∴ Area (BCED) = Area (ABMN) + Area (ACFG) [Using equations (3) and (7)]