NCERT Solutions Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.3

Exercise – 9.3

1. In Fig.9.23, E is any point on the median AD of a ΔABC. Show that ar (ABE) = ar(ACE).

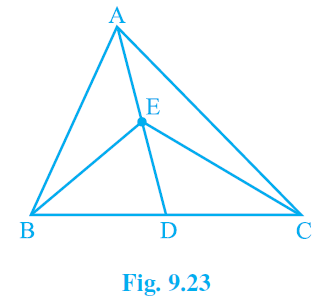
Answer – Given : AD is the median of ΔABC.
∴, it will divide ΔABC into two triangles of equal area.
∴ Area (ABD) = Area (ACD)       ————— (i)
also,
ED is the median of ΔABC.
∴ Area (EBD) = Area (ECD)      ————— (ii)
Subtracting (ii) from (i),
Area (ABD) – Area (EBD) = Area (ACD) – Area (ECD)
⇒ Area (ABE) = Area (ACE)

2. In a triangle ABC, E is the mid-point of median AD. Show that ar(BED) = ¼ ar(ABC).
Answer – Let ABC be a triangle and AD is the median of $\Delta ABC,$E is the mid point of AD.

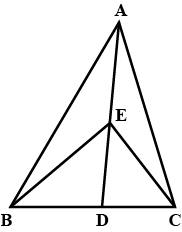
To prove : Area (BED) = Area (ABC)
In $\Delta ABC$,
$Area\; (ABD)=\; Area(ACD)$          ——————- (1)
In $\Delta ABD$, BE is the median
$Area\; (ABE)=\; Area(BED)$          ——————- (2)
Now, ar (ABD) = Area (BED)
= 2 Area (BED)                       ——————- (3)
Area (ABC) = Area (ABD) + Area (ACD)
Area (ABD) = 2 Area (ABD)                    using (1)
Area (ABC) = 2 × 2 Area (BED)              using (2)
Area (ABC) = 4 Area (BED)
∴ Area (BED) = ​Area (ABC)
Hence it is proved.

3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer – We know that the diagonals of a parallelogram bisect each other.
Also, the median of a triangle divides it into two triangles of equal areas. By the use of these observations, we can get the required result.
Let’s draw a diagram according to the question statement. 

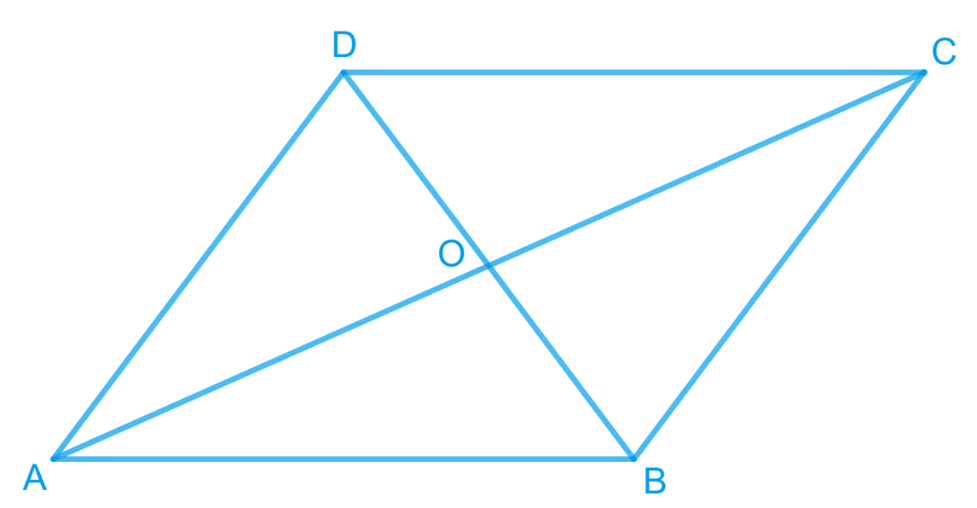
O is the midpoint of AC and BD. (Diagonals bisect each other)
In ΔABC, BO is the median.
∴ Area (AOB) = Area (BOC)           ————— (i)
also,
In ΔBCD, CO is the median.
∴ Area (BOC) = Area (COD)          ————— (ii)
In ΔACD, OD is the median.
∴ Area (AOD) = Area (COD)          ————— (iii)
In ΔABD, AO is the median.
∴ Area (AOD) = Area (AOB)          ————— (iv)
From equations (i), (ii), (iii) and (iv), we get
Area (BOC) = Area (COD) = Area (AOD) = Area (AOB)
Hence, we get the diagonals of a parallelogram that divide it into four triangles of equal area.

4. In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If the line-segment CD is bisected by AB at O, show that ar(ABC) = ar(ABD).

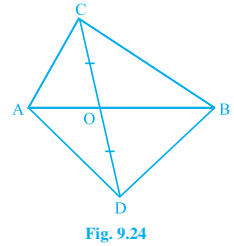
Answer – AB bisects CD at O signifies that O is the mid-point of CD. AO and BO are medians of triangles ADC and BDC.
Also, the median divides the triangle into two triangles of equal areas. 
Consider ΔACD.
Line-segment CD is bisected by AB at O. Therefore, AO is the median of ΔACD.
∴ Area (ΔACO) = Area (ΔADO)            —————(1)
Similarly, Considering ΔBCD , BO is the median.
∴ Area (ΔBCO) = Area (ΔBDO)          ————— (2)
Adding equation (1) and equation (2), we obtain
Area (ΔACO) + Area (ΔBCO) = Area (ΔADO) + Area (ΔBDO)
⇒ Area (ΔABC) = Area (ΔABD)

5. D, E and F are, respectively, the midpoints of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram
(ii) ar(DEF) = ¼ ar(ABC)
(iii) ar (BDEF) = ½ ar(ABC)
Answer – The midpoint theorem states that the line joining the mid-points of two sides of a triangle is parallel to the third side and half of its length.
If one pair of the opposite side in a quadrilateral is parallel and equal to each other then it is a parallelogram. Diagonals separate the parallelogram into two triangles of equal areas.
Let’s construct a diagram according to the given question.

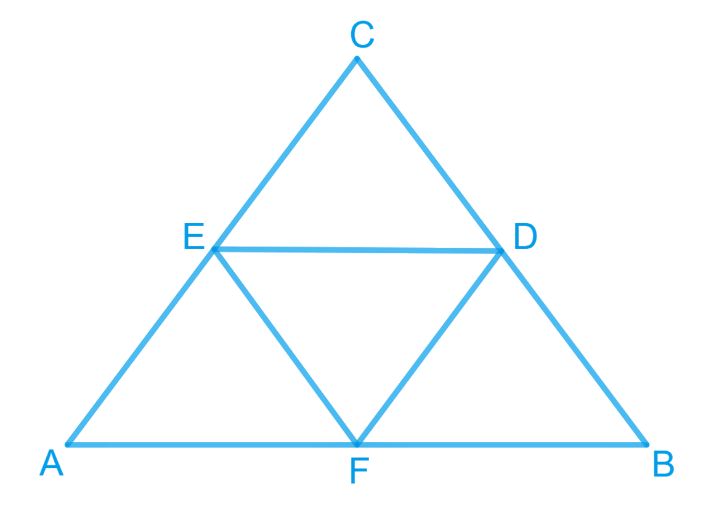
(i) BDEF is a parallelogram
In ΔABC,
EF || BC and EF = ½ BC (by the midpoint theorem)
also,
BD = ½ BC (D is the midpoint)
So, BD = EF
also,
BF and DE are parallel and equal to each other.
∴ the pair of opposite sides are equal in length and parallel to each other.
∴ BDEF is a parallelogram.

(ii) ar(DEF) = ¼ ar(ABC)
Proceeding from the result of (i),
BDEF, DCEF, and AFDE are parallelograms.
A diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area (ΔBFD) = Area (ΔDEF) (For parallelogram BDEF)     ——–— (i)
also,
Area (ΔAFE) = Area (ΔDEF) (For parallelogram DCEF)        ———— (ii)
Area (ΔCDE) = Area (ΔDEF) (For parallelogram AFDE)        ——–— (iii)
From (i), (ii) and (iii)
Area (ΔBFD) = Area (ΔAFE) = Area (ΔCDE) = Area (ΔDEF)
⇒ Area (ΔBFD) + Area (ΔAFE) + Area (ΔCDE) + Area (ΔDEF) = Area (ΔABC)
⇒ 4 Area (ΔDEF) = Area (ΔABC)
⇒ Area (DEF) = ¼ Area (ABC)

(iii) ar (BDEF) = ½ ar(ABC)
Area (parallelogram BDEF) = Area (ΔDEF) + Area (ΔBDE)
⇒ Area (parallelogram BDEF) = Area (ΔDEF) + Area (ΔDEF)
⇒ Area (parallelogram BDEF) = 2× Area (ΔDEF)
⇒ Area (parallelogram BDEF) = 2× ¼ Area (ΔABC)
⇒ Area (parallelogram BDEF) = ½ Area (ΔABC)

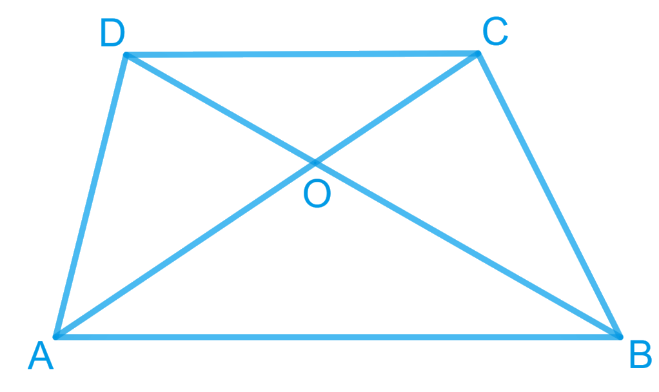
6. In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O, such that OB = OD.
If AB = CD, then show that

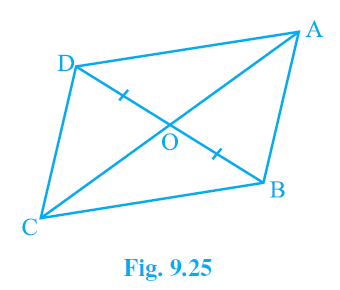
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

Answer – We can draw a perpendicular from vertices B and D on diagonal AC which will help us to make congruent triangles and we know that congruent triangles are always equal in areas.
If two triangles have the same base and also have equal areas, then these triangles must lie between the same parallels. 
Let us construct DN ⊥ AC and BM ⊥ AC.

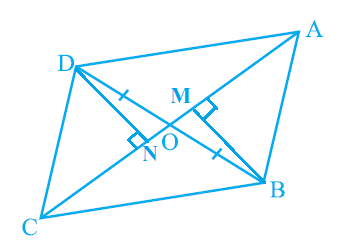
Given: OB = OD and AB = CD

(i) ar (DOC) = ar (AOB)
In ΔDOE and ΔBOF,
∠DEO = ∠BFO (Perpendiculars)
∠DOE = ∠BOF (Vertically opposite angles)
OD = OB (Given)
∴ ΔDOE ≅ ΔBOF by AAS congruence condition.
∴ DE = BF (By CPCT)            ———–— (i)
also,
Area (ΔDOE) = Area (ΔBOF) (Congruent triangles)  ———–— (ii)
Now,
In ΔDEC and ΔBFA,
∠DEC = ∠BFA (Perpendiculars)
CD = AB (Given)
DE = BF (From i)
∴ ΔDEC ≅ ΔBFA by RHS congruence condition.
∴ Area (ΔDEC) = Area (ΔBFA) (Congruent triangles)       ———–— (iii)
Adding (ii) and (iii),
Area (ΔDOE) + Area (ΔDEC) = Area (ΔBOF) + Area (ΔBFA)
⇒ Area (DOC) = Area (AOB)

(ii) ar (DCB) = ar (ACB)
Area (ΔDOC) = Area (ΔAOB)
Adding Area (ΔOCB) in LHS and RHS, we get
⇒ Area (ΔDOC) + Area (ΔOCB) = Area (ΔAOB) + Area (ΔOCB)
⇒ Area (ΔDCB) = Area (ΔACB)

(iii) DA || CB or ABCD is a parallelogram.
When two triangles have the same base and equal areas, the triangles will be in between the same parallel lines
Area (ΔDCB) = Area (ΔACB)
DA || BC           ————— (iv)
For quadrilateral ABCD, one pair of opposite sides are equal (AB = CD), and the other pair of opposite sides are parallel.
∴ ABCD is parallelogram.

7. D and E are points on sides AB and AC, respectively, of ΔABC such that ar(DBC) = ar(EBC). Prove that DE || BC.
Answer – If two triangles are on a common base and have equal areas, then they will lie between the same parallel lines.
Let’s draw the given triangle ABC.

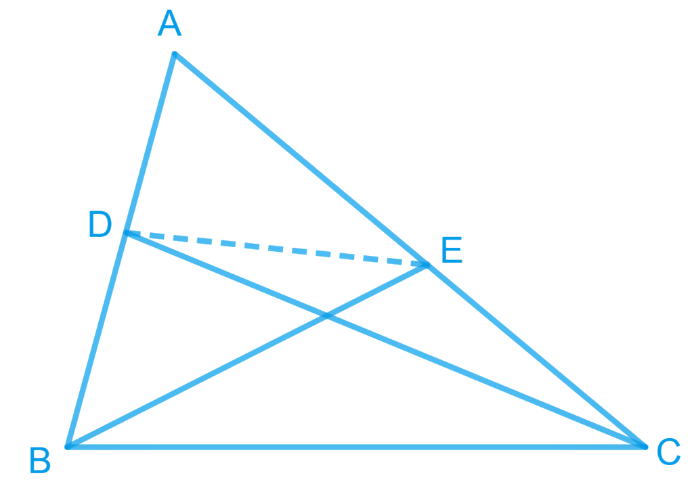
ΔDBC and ΔEBC are on the same base BC and also have equal areas.
∴ they will lie between the same parallel lines.
∴ DE || BC

8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar(ΔABE) = ar(ΔACF)
Answer – If a triangle and parallelogram are lying on the same base and between the same parallel lines, the area of the triangle will be equal to half of the area of a parallelogram.
Also, if two parallelograms are lying on the same base and between the same pair of parallel lines then both of them will have equal area.
Let’s draw points X and Y, intersected by line EF on sides AB and AC respectively.

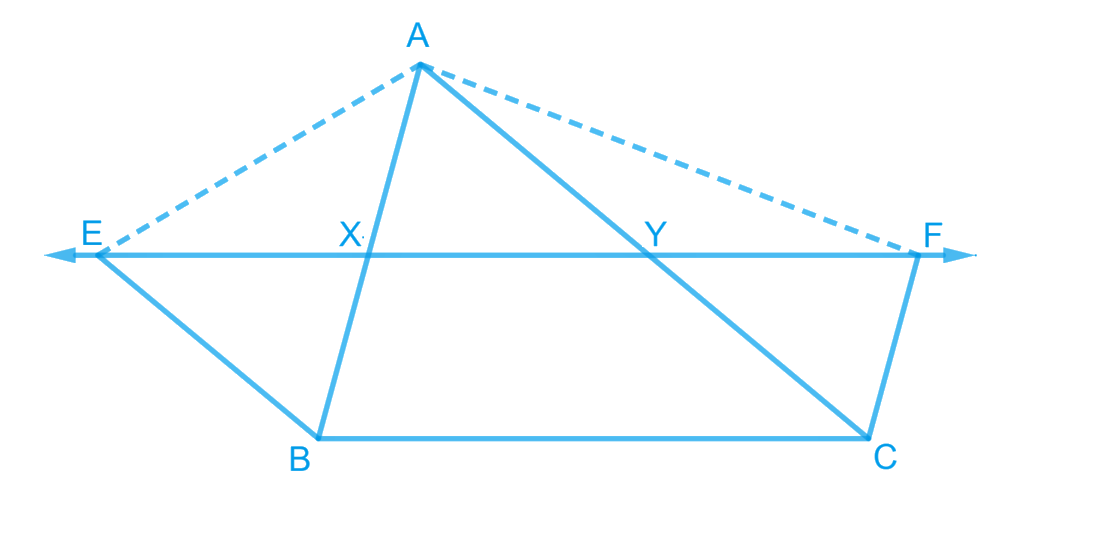
Let’s consider BCYE
It is given that, XY || BC so, EY || BC
Also, BE || AC so, BE || CY
Therefore, BCYE is a parallelogram.
Similarly, In BCFX
It is given that, XY || BC so, XF || BC
Since, CF || AB so, CF || BX
Therefore, BCFX is a parallelogram.
Parallelograms BCYE and BCFX are lying on the same base BC and between the same parallels BC and EF.
Therefore, According to Theorem 9.1: Parallelograms on the same base and between the same parallels are equal in area.
∴ Area (BCYE) = Area (BCFX)            —————- (i)
Now, Consider parallelogram BCYE and ΔAEB
They are lying on the same base BE and are between the same parallels BE and AC.
∴ Area (ΔABE) = 1/2 Area (BCYE)    —————- (ii)
Also, parallelogram BCFX and ΔACF are lying on the same base CF and existing between the same parallels CF and AB.
∴ Area (ΔACF) = 1/2 Area (BCFX)    —————- (iii)
From Equations (i), (ii), and (iii), we obtain
Area (ΔABE) = Area (ΔACF) proved.

9. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q, and then parallelogram PBQR is completed (see Fig. 9.26). Show that
ar(ABCD) = ar(PBQR).

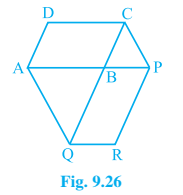
[Hint: Join AC and PQ. Now, compare ar(ACQ) and ar(APQ).]

Answer – Let us join AC and PQ.

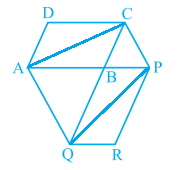
Area (△ACQ) = Area (△APQ) (On the same base AQ and between the same parallel lines AQ and CP)
⇒ Area (△ACQ) – Area (△ABQ) = Area (△APQ) – Area (△ABQ)
⇒ Area (△ABC) = Area (△QBP)             —————— (i)
AC and QP are diagonals ABCD and PBQR.
∴ Area (ABC) = ½ Area (ABCD)           —————-— (ii)
Area (QBP) = ½ Area (PBQR)              —————-— (iii)
From (ii) and (ii),
½ Area (ABCD) = ½ Area (PBQR)
⇒ Area (ABCD) = Area (PBQR)

10. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
Answer – Let’s draw the given trapezium ABCD

△DAC and △DBC lie on the same base DC and between the same parallels AB and CD.
Area (△DAC) = Area (△DBC)
⇒ Area (△DAC) – Area (△DOC) = Area (△DBC) – Area (△DOC)
⇒ Area (△AOD) = Area (△BOC)

11. In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
Show that

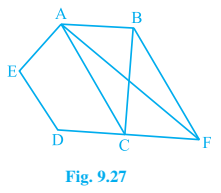
(i) ar(△ACB) = ar(△ACF)
(ii) ar(AEDF) = ar(ABCDE)

Answer –
(i) ar(△ACB) = ar(△ACF)
△ACB and △ACF lie on the same base AC and between the same parallels AC and BF.
∴ Area (△ACB) = Area (△ACF)

(ii) ar(AEDF) = ar(ABCDE)
⇒ Area (△ACB) + Area (ACDE) = Area (△ACF) + Area (ACDE)
⇒  Area (ABCDE) = Area (AEDF)

12. A villager, Itwaari, has a plot of land in the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given an equal amount of land in lieu of the land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Answer –  Let ABCD be the real shape of the quadrilateral field.

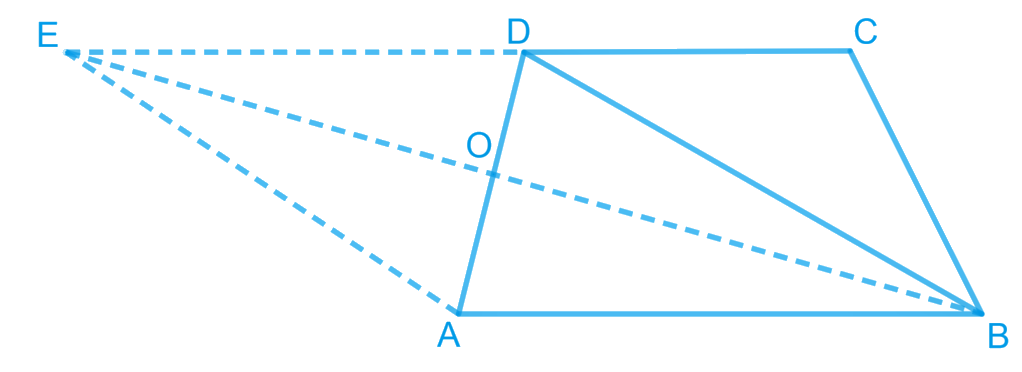
The proposal may be implemented as follows.
Join the BD diagonal and construct a line parallel to BD through point A.
Let that line meet further to the extended side CD of ABCD at point E.
Join BE and let BE and AD intersect each other at O.
Then, part ∆AOB is cut from the original field which is taken by the Gram Panchayat.
The new shape of the field will be ΔBCE. (See figure).
We have to prove that the area of ΔAOB is equal to the area of ΔDEO.
We can observe that ∆DEB and ∆DAB are lying on the same base BD and existing between the same parallels BD and AE.
According to Theorem 9.2: Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Therefore, Area (ΔDEB) = Area (ΔDAB)
Now, subtract Area (ΔDOB) from both side
Area (ΔDEB) – Area (ΔDOB) = Area (ΔDAB) – Area (ΔDOB)
Area (ΔDEO) = Area (ΔAOB)
Hence ΔAOB is the area of the plot taken by the gram Panchayat and an equivalent area of the plot that is ΔDEO is given to Itwaari so that the overall plot is triangular in shape that is ΔBCE.

13. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (△ADX) = ar (△ACY).
[Hint : Join CX.]

Answer – Let’s draw the given trapezium ABCD with AB || DC.

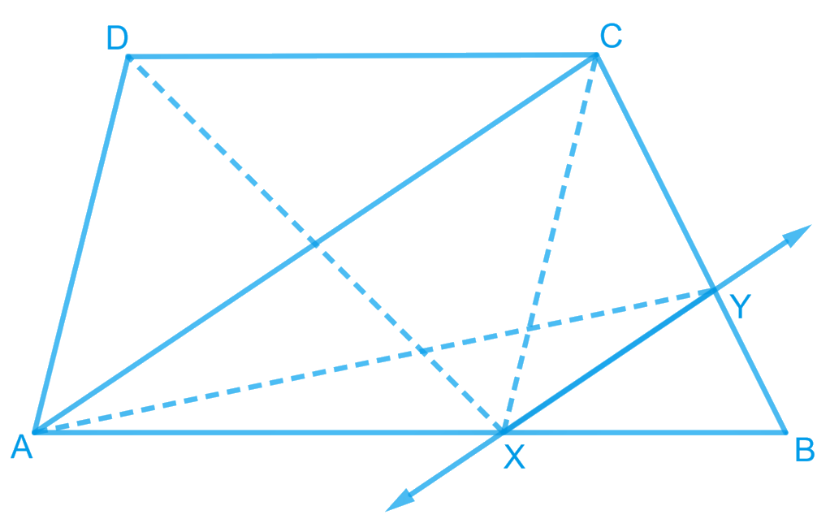
We observe that ΔADX and ΔACX are lying on the same base AX and are existing between the same parallels AB and DC.
According to Theorem 9.2: Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Therefore, Area (ΔADX) = Area (ΔACX)      —————(i)
Similarly, ΔACY and ΔACX are lying on the same base AC and are existing between the same parallels AC and XY.
Therefore, Area (ΔACY) = Area (ΔACX)      —————-(ii)
From Equations (i) and (ii), we obtain
Area (ΔADX) = Area (ΔACY)
Henced proved.

14. In Fig.9.28, AP || BQ || CR. Prove that ar(△AQC) = ar(△PBR).

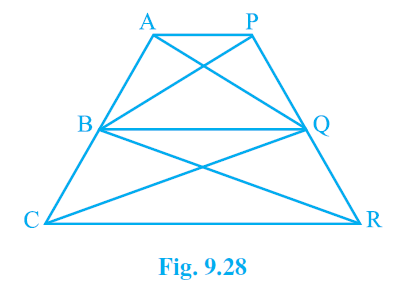
Answer – Given : AP || BQ || CR
To prove : Area (AQC) = Area (PBR)
Area (△AQB) = Area (△PBQ)       ———— (i) (Since they are on the same base BQ and between the same parallels AP and BQ.)
also,
Area (△BQC) = Area (△BQR)      ——–— (ii) (Since they are on the same base BQ and between the same parallels BQ and CR.)
Adding (i) and (ii),
Area (△AQB) + Area (△BQC) = Area (△PBQ) + Area (△BQR)
⇒ Area (△AQC) = Area (△PBR)

15. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD) = ar(△BOC). Prove that ABCD is a trapezium.
Answer – Let’s draw the given quadrilateral ABCD.

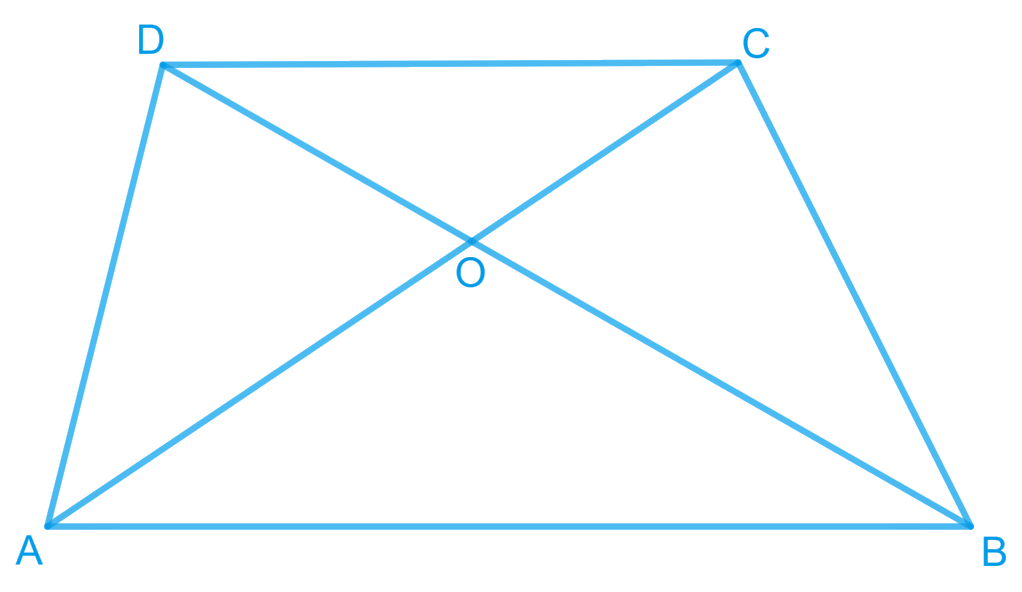
Given : ar(△AOD) = ar(△BOC)
To prove : ABCD is a trapezium.
Area (△AOD) = Area (△BOC)
⇒ Area (△AOD) + Area (△AOB) = Area (△BOC) + Area (△AOB)
⇒ Area (△ADB) = Area (△ACB)
Areas of △ADB and △ACB are equal.
∴ they must lie between the same parallel lines.
∴ AB || CD
∴ ABCD is a trapezium.

16. In Fig.9.29, ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

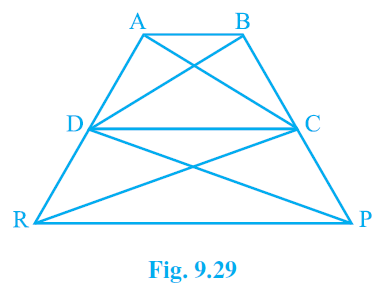
Answer – Given : ar(△DRC) = ar(△DPC),
ar(△BDP) = ar(△ARC)
To prove : ABCD and DCPR are trapeziums.
Area (△BDP) = Area (△ARC)
⇒ Area (△BDP) – Area (△DPC) = Area (△DRC)
⇒ Area (△BDC) = Area (△ADC)
∴ Area (△BDC) and Area (△ADC) are lying between the same parallel lines.
∴ AB || CD
ABCD is a trapezium.
Similarly,
Area (△DRC) = Area (△DPC).
∴ Area (△DRC) and Area (△DPC) are lying between the same parallel lines.
∴ DC || PR
∴ DCPR is a trapezium.