NCERT Solutions Class 9 Maths Chapter 8 Quadrilaterals Ex 8.1

Exercise – 8.1

1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Answer – Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
∴ 3x + 5x + 9x + 13x = 360°  [Angle sum property of a quadrilateral]
⇒ 30x = 360°
⇒ x = 360°/30 = 12°
∴ 3x = 3 × 12° = 36°
5x = 5 × 12° = 60°
9x = 9 × 12° = 108°
13x = 13 ×12° = 156°
⇒ The required angles of the quadrilateral are 36°, 60°, 108° and 156°.

2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Answer – Let ABCD be a parallelogram. To show that ABCD is a rectangle, we have to prove that one of its interior angles is 90°.

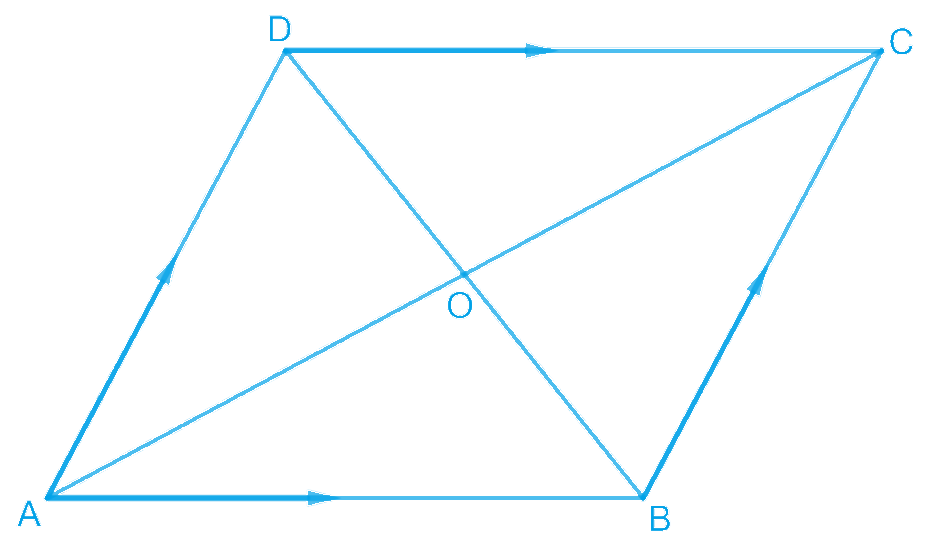
In ∆ABC and ∆DCB,
AC = DB     [Given]
AB = DC     [Opposite sides of a parallelogram]
BC = CB     [Common]
∴ ∆ABC ≅ ∆DCB [By SSS congruency]
⇒ ∠ABC = ∠DCB [By C.P.C.T.]  ————- (1)
Now, AB || DC and BC is a transversal. [ ∵ ABCD is a parallelogram]
∴ ∠ABC + ∠DCB = 180°      ————- (2) [Co-interior angles]
From (1) and (2), we have
∠ABC = ∠DCB = 90°
i.e., ABCD is a parallelogram having an angle equal to 90°.
∴ ABCD is a rectangle.

3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Answer – Let ABCD be a quadrilateral such that the diagonals AC and BD bisect each other at right angles at O.

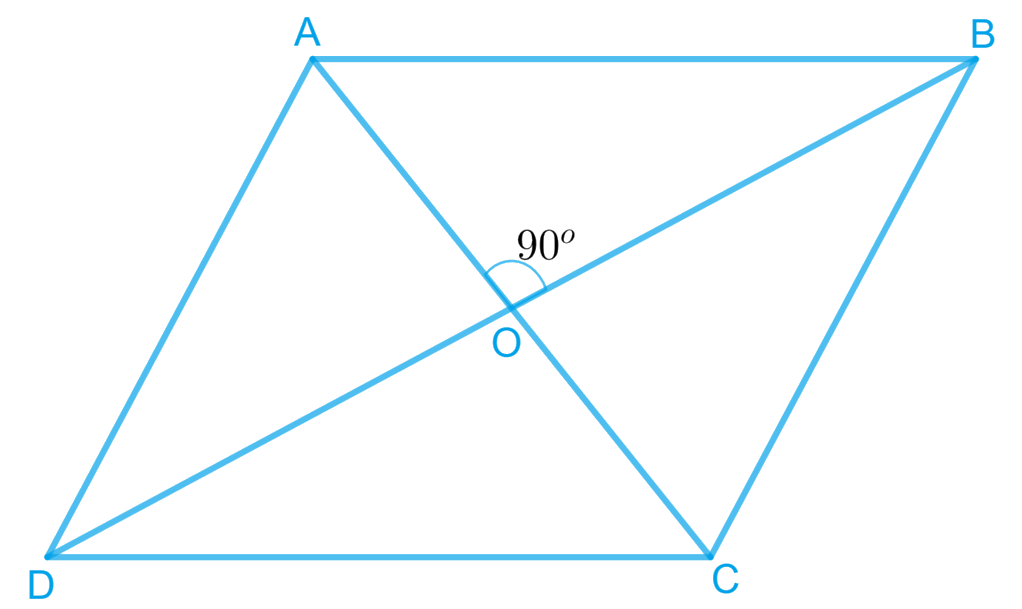
∴ In ∆AOB and ∆AOD, we have
AO = AO [Common]
OB = OD [O is the mid-point of BD]
∠AOB = ∠AOD [Each 90]
∴ ∆AQB ≅ ∆AOD [By,SAS congruency]
∴ AB = AD [By C.P.C.T.]       ————- (1)
Similarly, AB = BC                ————- (2)
BC = CD                                  ————- (3)
CD = DA                                 ————- (4)
∴ From (1), (2), (3) and (4), we have
AB = BC = CD = DA
Thus, the quadrilateral ABCD is a rhombus.
Alternatively : ABCD can be proved first a parallelogram then proving one pair of adjacent sides equal will result in rhombus.

4. Show that the diagonals of a square are equal and bisect each other at right angles.
Answer – Let ABCD be a square such that its diagonals AC and BD intersect at O.

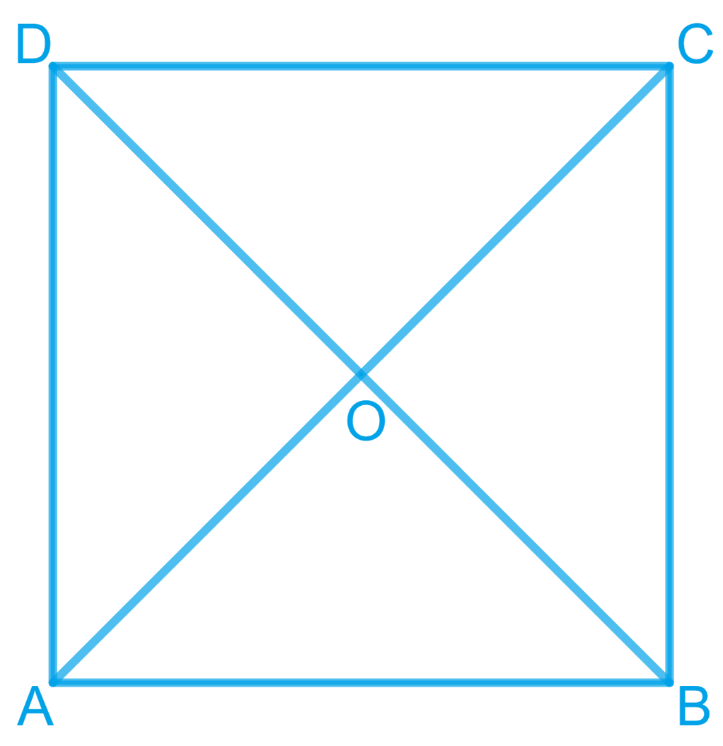
Thus, we have to prove AC = BD, OA = OC, OB = OD, and ∠AOB = 90°
Let ABCD be a square.
Let the diagonals AC and BD intersect each other at a point O.
In ΔABC and ΔDCB,
AB = DC (Sides of a square are equal to each other)
∠ABC = ∠DCB (All interior angles are of 90^o)
BC = CB (Common side)
∴ ΔABC ≅ ΔDCB (By SAS congruence rule)
∴ AC = DB (By CPCT)                 ———— (1)
Hence, the diagonals of a square are equal in length.
In ΔAOB and ΔCOD,
∠AOB = ∠COD (Vertically opposite angles)
∠ABO = ∠CDO (Alternate interior angles)
AB = CD (Sides of a square are always equal)
∴ ΔAOB ≅ ΔCOD (By AAS congruence rule)
∴ AO = CO and OB = OD (By CPCT)            ———— (2)
Hence, the diagonals of a square bisect each other.
In ΔAOB and ΔCOB,
As we had proved that diagonals bisect each other,
Therefore, AO = CO
AB = CB (Sides of a square are equal)
BO = BO (Common)
∴ ΔAOB ≅ ΔCOB (By SSS congruency)
∴ ∠AOB = ∠COB (By CPCT)              ——— (3)
However, ∠AOB + ∠COB = 180° (Linear pair)
2∠AOB = 180° [From equation (3)]
∠AOB = 90°                                   ————- (4)
Hence, from equation (1), (2) and (4), we see that the diagonals of a square are equal and bisect each other at right angles.

5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Answer – Let us consider a quadrilateral ABCD in which the diagonals AC and BD intersect each other at O.

It is given that the diagonals of ABCD are equal and bisect each other at right angles.
Therefore, AC = BD, OA = OC, OB = OD, and ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
To prove ABCD is a square, we have to prove that ABCD is a parallelogram in which AB = BC = CD = AD, and one of its interior angles is 90°.
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
OB = OD (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite angles)
∴ ΔAOB ≅ ΔCOD (SAS congruence rule)
∴ AB = CD (By CPCT)                    ————– (1)
And, ∠OAB = ∠OCD (By CPCT)
However, these are alternate interior angles for line AB and CD and alternate interior angles are equal to each other only when the two lines are parallel.
Thus, AB || CD                              ————– (2)
From Equations (1) and (2), we obtain ABCD is a parallelogram.
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Each angle is 90°)
OD = OD (Common)
∴ ΔAOD ≅ ΔCOD (SAS congruence rule)
∴ AD = DC (By CPCT)                 ————– (3)
However, AD = BC and AB = CD (Opposite sides of parallelogram ABCD are equal)
∴ AB = BC = CD = DA
Therefore, all the sides of quadrilateral ABCD are equal to each other.
In ΔADC and ΔBCD,
AD = BC (Already proved)
AC = BD (Given)
DC = CD (Common)
∴ ΔADC ≅ ΔBCD (SSS Congruence rule)
∴ ∠ADC = ∠BCD (By CPCT)
However, ∠ADC + ∠BCD = 180°(Co-interior angles)
∠ADC + ∠ADC = 180°
2∠ADC = 180°
∴ ∠ADC = 90°
One of the interior angles of quadrilateral ABCD is a right angle.
Thus, we have obtained that ABCD is a parallelogram where AB = BC = CD = AD and one of its interior angles is 90°.
Therefore, ABCD is a square.

6. Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that

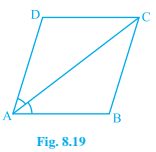
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
Answer – Given: The diagonal AC of a parallelogram ABCD bisects ∠A.
(i) it bisects ∠C also
ABCD is a parallelogram.
∠DAC = ∠BCA (Alternate interior angles)   ————– (1)
∠BAC = ∠DCA (Alternate interior angles)   ————– (2)
However, it is given that AC bisects ∠A.
∠DAC = ∠BAC                                            ————– (3)
From equations (1), (2), and (3), we obtain
∠DCA  = ∠BAC = ∠DAC = ∠BCA          ————– (4)
Thus, ∠DCA = ∠BCA
Hence, AC bisects ∠C.

(ii) ABCD is a rhombus.
From Equation (4), we obtain
∠DAC = ∠DCA
DA = DC (Side opposite to equal angles are equal)
However, DA = BC and AB = CD (Opposite sides of a parallelogram  are equal)
Thus, AB = BC = CD = DA
Hence, ABCD is a rhombus.

7. ABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠C and diagonal BD bisects ∠B as well AS ∠D.
Answer – Given: ABCD is a rhombus.

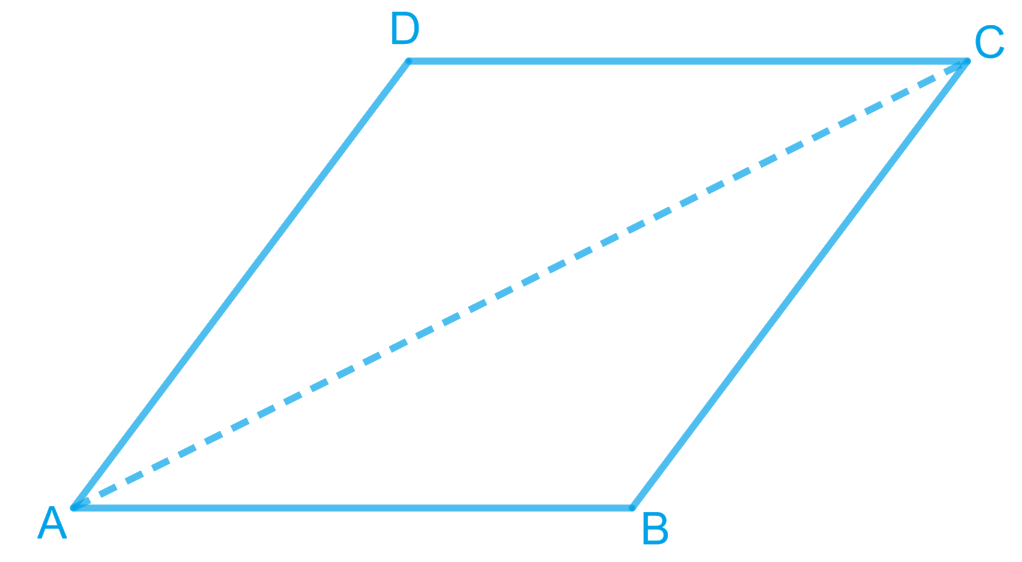
Let us join AC.
In ΔABC, BC = AB (Sides of a rhombus are equal to each other)
So, ∠BAC = ∠BCA (Angles opposite to equal sides of a triangle are equal)          ———–(1)
However,
∠BAC = ∠DCA (Alternate interior angles for parallel lines AB and CD)             ————-(2)
From equation (1) and (2), ∠BCA = ∠DCA
Therefore, AC bisects ∠C.
Also, ∠BCA = ∠DAC (Alternate interior angles for parallel lines BC and DA)
Thus, ∠BAC = ∠DAC
Therefore, AC bisects ∠A as well as ∠C.
Similarly, it can be proved that BD bisects ∠B and ∠D as well.

8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
Answer – We have a rectangle ABCD such that AC bisects ∠A as well as ∠C.

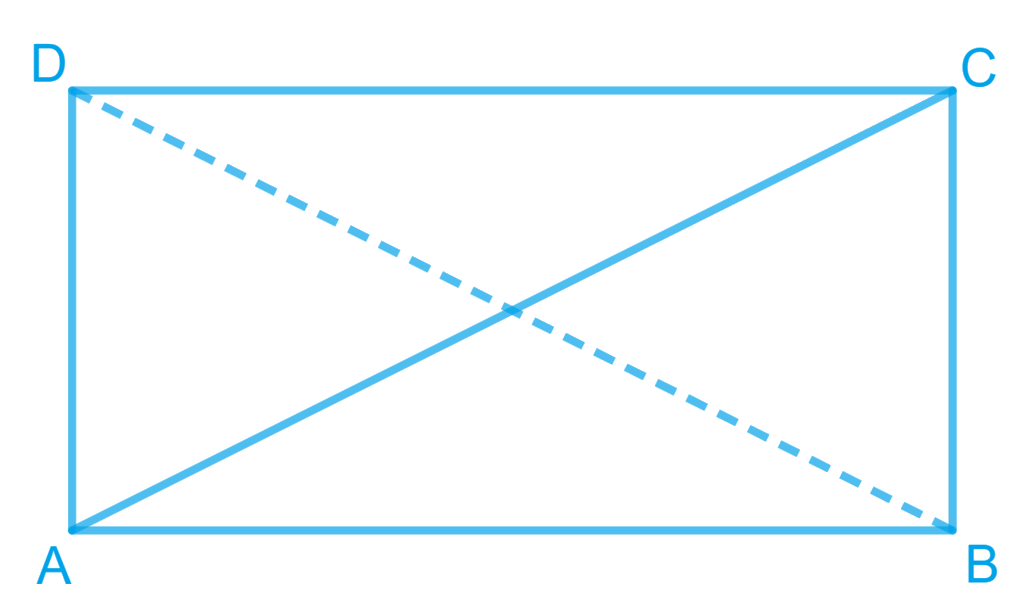
(i) ABCD is a square
We are given that ABCD is a rectangle, so
∠A = ∠C
⇒ ∠A = ∠C
⇒ ∠DAC = ∠DCA (Given that AC bisects ∠A and ∠C)
Thus, CD = DA (Sides opposite to equal angles are also equal)
However, DA = BC and AB = CD (Opposite sides of a rectangle are equal)
Thus AB = BC = CD = DA
ABCD is a rectangle and all the sides are equal. Hence, ABCD is a square.

(ii) diagonal BD bisects ∠B as well as ∠D.
Let us join BD
Since ABCD is square, AB || CD and BC || AD
In ΔBCD,
BC = CD (Sides of a square are equal to each other)
∠CDB = ∠CBD (Angles opposite to equal sides are equal)   ———— (1)
However, ∠CDB = ∠ABD (Alternate interior angles as AB || CD)    ———— (2)
From equations (1) and (2), ∠CBD = ∠ABD
Thus, BD bisects ∠B.
Also, ∠CBD = ∠ADB (Alternate interior angles for BC || AD) ———— (3)
So, using equations (1) and (3), ∠ADB = ∠CDB
Hence, BD bisects ∠D and ∠B.

9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that

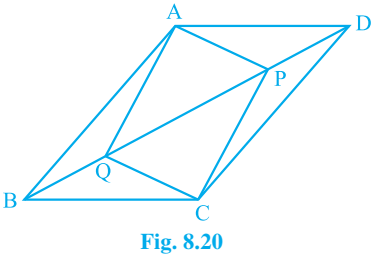
(i) Δ APD ≅ Δ CQB
(ii) AP = CQ
(iii) Δ AQB ≅ Δ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram

Answer – Given: ABCD is a parallelogram and DP = BQ

(i) Δ APD ≅ Δ CQB
In ΔAPD and ΔCQB,
∠ADP = ∠CBQ (Alternate interior angles for BC || AD)
AD = CB (Opposite sides of parallelogram ABCD)
DP = BQ (Given)
∴ ΔAPD ≅ ΔCQB (Using SAS congruence rule)

(ii) AP = CQ
Since ΔAPD ≅ ΔCQB,
∴ AP = CQ (By CPCT)

(iii) Δ AQB ≅ Δ CPD
In ΔAQB and ΔCPD,
AB = CD (Opposite sides of parallelogram ABCD)
∠ABQ = ∠CDP (Alternate interior angles for AB || CD)
BQ = DP (Given)
∴ ΔAQB ≅ ΔCPD (Using SAS congruence rule)

(iv) AQ = CP
Since ΔAQB ≅ ΔCPD,
∴ AQ = CP (CPCT)

(v) APCQ is a parallelogram
From the result obtained in (ii) and (iv), AQ = CP and AP = CQ
Since opposite sides in quadrilateral APCQ are equal to each other, thus APCQ is a parallelogram.

10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see figure). Show that

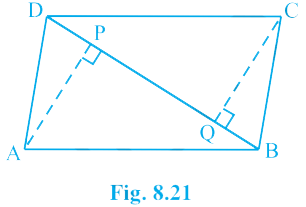
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ

Answer – Given: ABCD is a parallelogram and AP ⊥ DB, CQ ⊥ DB
(i) ΔAPB ≅ ΔCQD
In ΔAPB and ΔCQD,
∠APB = ∠CQD (Each 90°)
AB = CD (Opposite sides of parallelogram ABCD)
∠ABP = ∠CDQ (Alternate interior angles as AB || CD)
∴ ΔAPB ≅ ΔCQD (By AAS congruency)

(ii) AP = CQ
By using the result ΔAPB ≅ ΔCQD., we obtain AP = CQ (By CPCT)

11. In ∆ABC and ∆DEF, AB = DE, AB || DE, BC – EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F, respectively (see figure). Show that

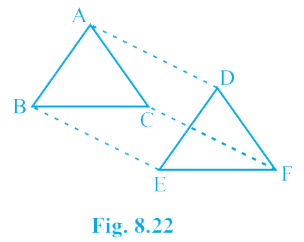
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF

Answer – Given: In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF.
(i) quadrilateral ABED is a parallelogram
It is given that AB = DE and AB || DE
If one pair of opposite sides of a quadrilateral are equal and parallel to each other, then it will be a parallelogram.
Therefore, quadrilateral ABED is a parallelogram.

(ii) quadrilateral BEFC is a parallelogram
It is given that BC = EF and BC || EF
Therefore, quadrilateral BEFC is a parallelogram.

(iii) AD || CF and AD = CF
As we had observed that ABED and BEFC are parallelograms, therefore
AD = BE  and AD || BE (Opposite sides of a parallelogram are equal and parallel)
BE = CF and BE || CF (Opposite sides of a parallelogram are equal and parallel)
Thus, AD = BE = CF and AD || BE || CF
∴ AD = CF and AD || CF (Lines parallel to the same line are parallel to each other)

(iv) quadrilateral ACFD is a parallelogram
As we had observed that one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and parallel to each other, therefore, it is a parallelogram.

(v) AC = DF
As ACFD is a parallelogram, therefore, the pair of opposite sides will be equal and parallel to each other
∴ AC || DF and AC = DF

(vi) ∆ABC ≅ ∆DEF
∆ABC and ∆DEF,
AB = DE (Given)
BC = EF (Given)
AC = DF (Since ACFD is a parallelogram)
∴ ∆ABC ≅ ∆DEF (By SSS congruence rule)

12. ABCD is a trapezium in which AB || CD and AD = BC (see figure). Show that

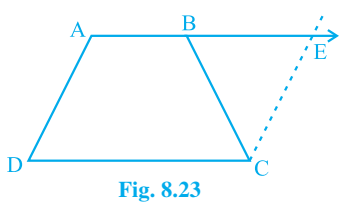
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E].

Answer – Let us join BD and AC in the figure shown below. ADCE is a parallelogram.

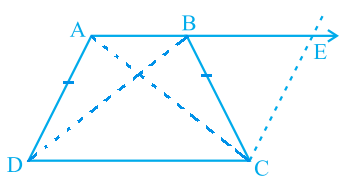
(i) ∠A = ∠B
AD = CE (Opposite sides of parallelogram AECD are equal)
However, AD = BC (Given)
Therefore, BC = CE
∠CEB = ∠CBE (Angles opposite to equal sides in a triangle are also equal)
Consider, parallel lines AD and CE where AE is the transversal.
∠BAD + ∠CEB = 180° [Co-Interior angles]
∠BAD + ∠CBE = 180°  ————- (1) [Since, ∠CEB = ∠CBE]
However, ∠ABC + ∠CBE = 180° (Linear pair angles) ————- (2)
From Equations (1) and (2), we see that
∠BAD = ∠ABC
Thus, ∠A = ∠B

(ii) ∠C = ∠D
AB || CD
∠A + ∠D = 180° (Angles on the same side of the transversal)
Also, ∠C + ∠B = 180° (Angles on the same side of the transversal)
∴ ∠A + ∠D = ∠C + ∠B
However, ∠A = ∠B [Using the result obtained in (i)]
∴ ∠C = ∠D

(iii) ∆ABC ≅ ∆BAD
In ∆ABC and ∆BAD,
AB = BA (Common side)
BC = AD (Given)
∠B = ∠A (Proved before)
∴ ∆ABC ≅ ∆BAD (SAS congruence rule)

(iv) diagonal AC = diagonal BD
Since ∆ABC ≅ ∆BAD,
∴ AC = BD (By CPCT)