NCERT Solutions Class 9 Maths Chapter 7 Triangles Ex 7.5

Exercise – 7.5

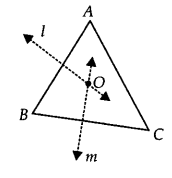
1. ABC is a triangle. Locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC.
Answer – Let us consider a ∆ABC.
Draw l, the perpendicular bisector of AB.
Draw m, the perpendicular bisector of BC.
Let the two perpendicular bisectors l and m meet at O.
O is the required point which is equidistant from A, B and C.

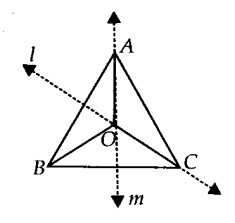
Note: If we draw a circle with centre O and radius OB or OC, then it will pass through A, B and C. The point O is called circumcentre of the triangle.

2. In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Answer – Let us consider a ∆ABC.

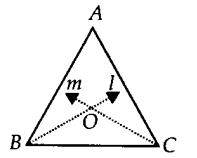
Draw m, the bisector of ∠C.
Let the two bisectors l and m meet at O.
Thus, O is the required point which is equidistant from the sides of ∆ABC.
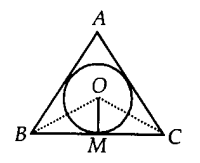
Note: If we draw OM ⊥ BC and draw a circle with O as centre and OM as radius, then the circle will touch the sides of the triangle. Point O is called incentre of the triangle.

3. In a huge park, people are concentrated at three points (see figure)

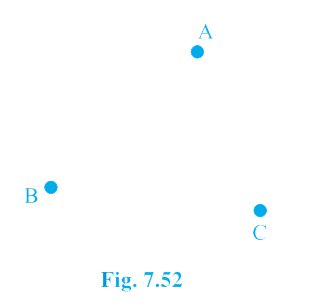
A: where these are different slides and swings for children.
B: near which a man-made lake is situated.
C: which is near to a large parking and exist.
Where should an ice-cream parlor be set? up so that maximum number of persons can approach it?
[Hint The parlour should be equidistant from A, B and C.]
Answer –  Let us join A and B, and draw l, the perpendicular bisector of AB.
Now, join B and C, and draw m, the perpendicular bisector of BC. Let the perpendicular bisectors l and m meet at O.
The point O is the required point where the ice cream parlour be set up.

Note: If we join A and C and draw the perpendicular bisector, then it will also meet (or pass through) the point O.

4. Complete the hexagonal and star shaped Rangolis’ [see Fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

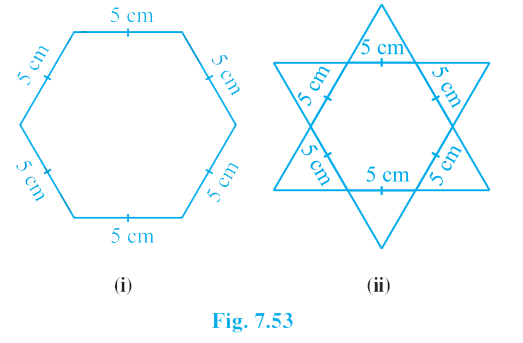
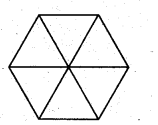
Answer – We first divide the hexagon into six equilateral triangles of side 5cm as follow.

We take one triangle from six equilateral triangles as shown above and make as many equilateral triangles of one side 1 cm as shown in the figure.

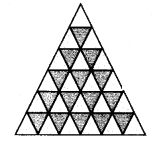
The number of equilateral triangles of side 1 cm = 1 + 3 + 5 + 7 + 9 = 25
So, the total number of triangles in the hexagon = 6 × 25 = 150
To find the number of triangles in the Fig. (ii), we adopt the same procedure.
So, the number of triangles in the Fig. (ii) = 12 × 25 = 300
Hence, Fig. (ii) has more triangles.