NCERT Solutions Class 9 Maths
Chapter – 6 (Lines And Angles)
The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 6 Lines And Angles Exercise 6.3 has been provided here to help the students in solving the questions from this exercise.
Chapter 6: Lines and Angles
Exercise – 6.3
1. In Fig. 6.39, sides QP and RQ of ΔPQR are produced to points S and T, respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
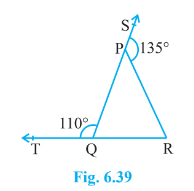
Answer – It is given in the question that:
∠SPR = 135° and, ∠PQT = 110o
Now, according to the question,
∠SPR + ∠QPR = 180° (SQ is a straight line)
135° + ∠QPR = 180°
∠QPR = 45°
And,
∠PQT + ∠PQR = 180° (TR is a straight line)
110° + ∠PQR = 180°
∠PQR = 70°
Now,
∠PQR + ∠QPR + ∠PRQ = 180° (Sum of the interior angles of the triangle)
70° + 45° + ∠PRQ = 180°
115° + ∠PRQ = 180°
∠PRQ = 65°
2. In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY, respectively of Δ XYZ, find ∠OZY and ∠YOZ.
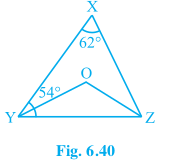
Answer – We know the sum of the interior angles of the triangle.
So, ∠YXZ +∠XYZ +∠XZY = 180°
62°+ 54° +∠XZY = 180°
116° + ∠XZY = 180°
∠XZY = 180° – 116°
∠XZY = 64°
Now, we know that ZO is the bisector, so,
∠OZY = ½ ∠XZY
∴ ∠OZY = × 32°
Similarly, YO is a bisector, and so,
∠OYZ = ½ ∠XYZ
∠OYZ = × 54°
∠OYZ = 27°
Now, as the sum of the interior angles of the triangle,
∠OZY +∠OYZ +∠O = 180°
∠O = 180° – 32° – 27°
Hence, ∠O = 121°
3. In Fig. 6.41, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
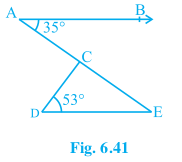
Answer – We know that AE is a transversal since AB || DE
Here ∠BAC and ∠AED are alternate interior angles.
Hence, ∠BAC = ∠AED
It is given that ∠BAC = 35°
∠AED = 35°
Now, consider the triangle CDE. We know that the sum of the interior angles of a triangle is 180°.
∴ ∠DCE + ∠CED + ∠CDE = 180°
∠DCE + 35° + 53° = 180°
∠DCE + 88° = 180°
∠DCE = 180° – 88°
∠DCE = 92°
Hence, ∠DCE = 92°
4. In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95°, and ∠TSQ = 75°, find ∠SQT.
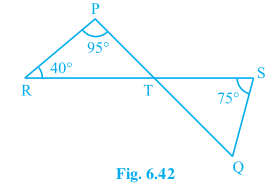
Answer – Consider triangle PRT.
∠PRT + ∠RPT + ∠PTR = 180°
∠PTR + 95° + 40° = 180°
∠PTR + 135° = 180°
∠PTR = 180° – 135°
∠PTR = 45°
Now ∠PTR will be equal to ∠STQ as they are vertically opposite angles.
So, ∠PTR = ∠STQ = 45°
Again, in triangle STQ,
∠TSQ + ∠PTR + ∠SQT = 180°
75° + 45° + ∠SQT = 180°
120° + ∠SQT = 180°
∠SQT = 180° – 120°
∠SQT = 60°
5. In Fig. 6.43, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
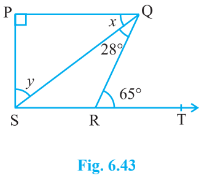
Answer – PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°
We know when two parallel lines are cut by a transversal, alternate interior angles formed are equal.
According to the angle sum property of a triangle, sum of the interior angles of a triangle is 360°.
Since, PQ || SR and QR is the transversal,
∠PQR = ∠QRT [Alternate interior angles]
∠PQS + ∠SQR = ∠QRT [From figure]
x + 28° = 65°
x = 65° – 28°
x = 37°
Now, in △PQS
∠PQS + ∠PSQ + ∠QPS = 180° [Angle sum property of a triangle]
37° + y + 90° = 180° [Since. ∠QPS = 90°]
y = 180° – 127°
y = 53°
Hence, x = 37° and y = 53°
6. In Fig. 6.44, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = ½ ∠QPR.
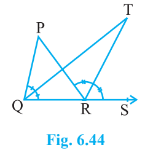
Answer – Given: TQ and TR are the bisectors of ∠PQR and ∠PRS respectively
To Prove: ∠QTR = 1/2 ∠QPR
According to the exterior angle theorem of a triangle, if a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
∠PRS = 2∠TRS ————– (i) [Since TR is the angle bisector of ∠PRS]
∠PQR = 2∠TQR ————— (ii) [Since TQ is the angle bisector of ∠PQR]
Now, in △TQR
∠TRS = ∠TQR +∠QTR [Exterior angle theorem of a triangle]
∠QTR = ∠TRS – ∠TQR —————– (iii)
Similarly, in △PQR
∠PRS = ∠QPR + ∠PQR [Exterior angle theorem of a triangle]
2∠TRS = ∠QPR + 2∠TQR [From (i) and (ii)]
∠QPR = 2∠TRS – 2∠TQR
∠QPR = 2(∠TRS – ∠TQR)
∠QPR = 2∠QTR [From (iii)]
∠QTR = 1/2 ∠QPR
Hence proved, ∠QTR = 1/2 ∠QPR.

Leave a Reply