NCERT Solutions Class 9 Maths
Chapter – 5 (Introduction to Euclids Geometry)
The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 5 Introduction to Euclids Geometry Exercise 5.2 has been provided here to help the students in solving the questions from this exercise.
Chapter 5: Introduction to Euclid Geometry
Exercise – 5.2
1. How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Answer – Euclid’s fifth postulate: Given a line L and a point P not on the line, exactly one line can be drawn through P which is parallel to L.
Let’s understand this.
For every line ‘l’ and for every point ‘P’ not lying on ‘l’, there exist a unique line ‘m’ passing through ‘P’ and parallel to ‘l’. This is called ‘Playfair’s Axiom’.
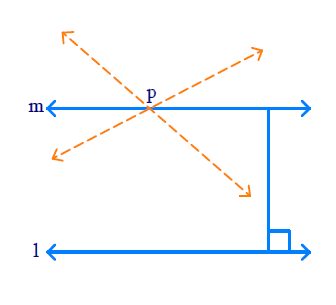
- ‘l’ is a line and ‘p’ is a point not lying on ’l’.
- We can draw infinite lines through ‘p’ but there is only one line unique which is parallel to ‘l’ and passes through ‘p’.
- Take any point on ‘l’ and draw a line to ‘m’. Measure these distances.
- We know that it is the same everywhere, so these lines ‘l’ and ‘m’ do not meet anywhere.
- Hence, the two lines ‘l’ and ‘m’ are parallel.
2. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Answer – Yes, according to Euclid’s fifth postulate when line x falls on straight line y and z such that sum of the interior angles on one side of line x is two right angles.
∴ ∠1 + ∠2 = 180∘.
Then, line y and line z on producing further will meet in the side of ∠1 and ∠2 which is less than 180∘.
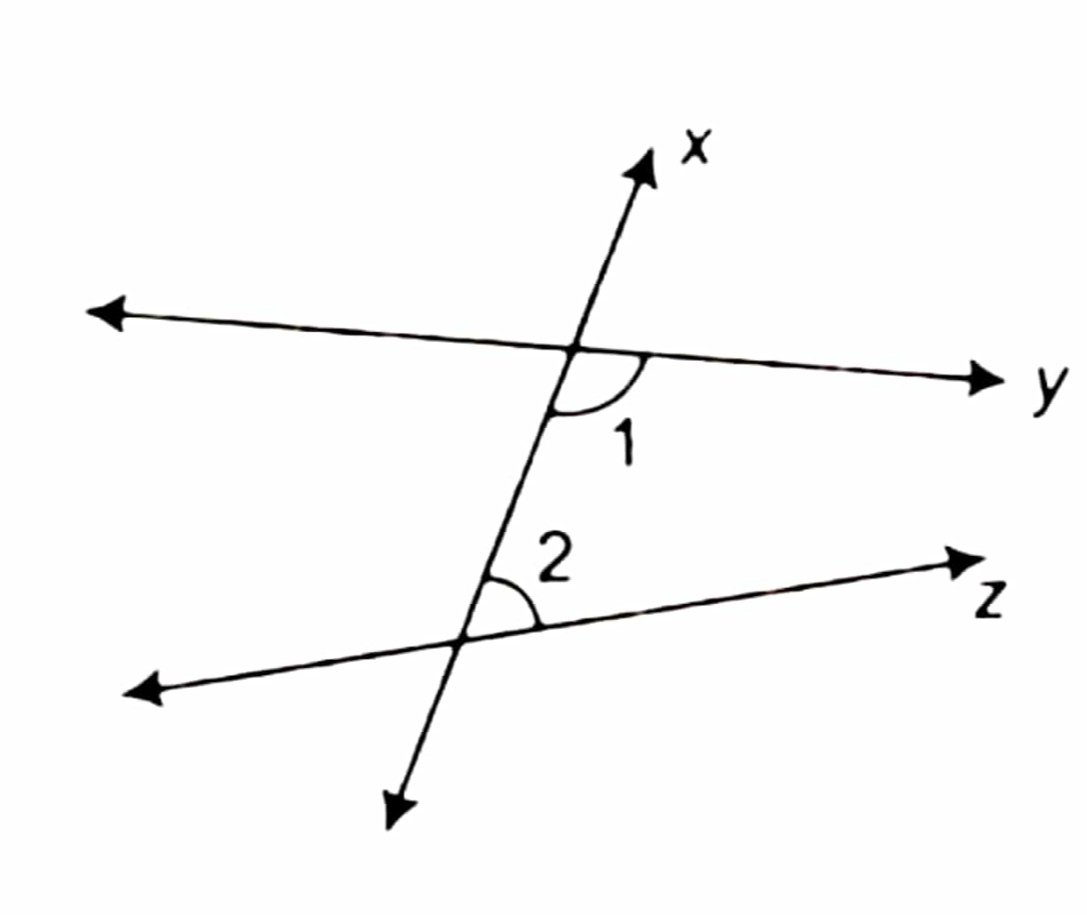
We find that the lines which are not according to Euclid’s fifth postulate.
∴ ∠1 + ∠2 = 180∘, do not intersect.
So, the lines y and z never meet and are, therefore, parallel.

Leave a Reply