NCERT Solutions Class 9 Maths
Chapter – 5 (Introduction to Euclids Geometry)
The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 5 Introduction to Euclids Geometry Exercise 5.1 has been provided here to help the students in solving the questions from this exercise.
Chapter 5: Introduction to Euclid Geometry
Exercise – 5.1
1. Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
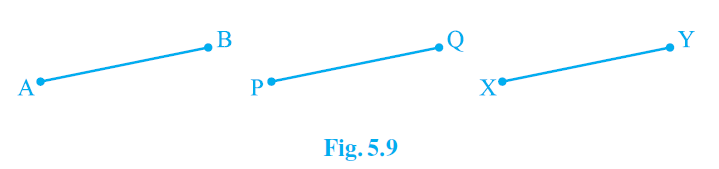
(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.
Answer –
(i) Only one line can pass through a single point.
(False) There can be infinite number of lines that can be drawn through a single point. Hence, the statement mentioned is False
(ii) There are an infinite number of lines which pass through two distinct points.
(False) Through two distinct points, there can be only one line that can be drawn. Hence, the statement mentioned is False
(iii) A terminated line can be produced indefinitely on both the sides.
(True) A line that is terminated can be indefinitely produced on both sides as a line can be extended on both its sides infinitely. Hence, the statement mentioned is True.
(iv) If two circles are equal, then their radii are equal.
(True) The radii of two circles are equal when the two circles are equal. The circumference and the centre of both the circles coincide; and thus, the radius of the two circles should be equal. Hence, the statement mentioned is True.
(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.
(True) According to Euclid’s 1st axiom- “Things which are equal to the same thing are also equal to one another”. Hence, the statement mentioned is True.
2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines
(ii) perpendicular lines
(iii) line segment
(iv) radius of a circle
(v) square
Answer – We have to define ‘Ray’, ‘Straight line’ and a ‘point’.
Ray: A part of a line, which starts at a point (Here A) and goes off in a particular direction to infinity possibly through a second point (B in this case).
Straight Line: The basic concept about a line is that it should be straight, and it can be extended infinitely in both directions.
Point: A small dot made by a sharp pencil on a sheet of paper gives an idea about a point.
(i) Parallel lines – Parallel lines are those lines which never intersect each other and are always at a constant perpendicular distance between each other. Parallel lines can be two or more lines.
(ii) Perpendicular lines – Perpendicular lines are those lines which intersect each other in a plane at right angles. The lines are said to be perpendicular to each other.
(iii) Line segment – When a line cannot be extended any further because of its two end points, then the line is known as a line segment. A line segment has 2 end points.
(iv) Radius of circle – A radius of a circle is the line from any point on the circumference of the circle to the center of the circle.
(v) Square – A quadrilateral in which all the four sides are said to be equal, and each of its internal angles is a right angle, is called square.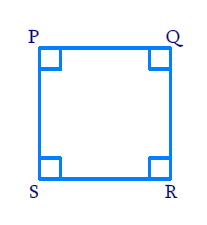
3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
Answer – There are several undefined terms which we should keep in mind. They are consistent, because they deal with two different situations:
(i) says that the given two points A and B, there is a point C lying on the line in between them;
(ii) says that given A and B, we ca take C not lying on the line through A and B. These ‘postulates’ do not follow from Euclid’s postulates. However, they follow from axiom stated as given two distinct points; there is a unique line that passes through them.
4. If a point C lies between two points A and B such that AC = BC, then prove that AC = ½ AB. Explain by drawing the figure.
Answer –
Given that, AC = BC
Now, adding AC both sides.
L.H.S + AC = R.H.S + AC
AC + AC = BC+ AC
2AC = BC+AC
We know that, BC+AC = AB (as it coincides with line segment AB)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal.)
⇒ AC = (½)AB.
5. In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Answer –
Let, AB be the line segment
Assume that points P and Q are the two different mid points of AB.
Now,
∴ P and Q are midpoints of AB.
Therefore,
AP = PB and AQ = QB.
also,
PB + AP = AB (as it coincides with line segment AB)
Similarly, QB+AQ = AB.
Now,
Adding AP to the L.H.S and R.H.S of the equation AP = PB
We get, AP+AP = PB+AP (If equals are added to equals, the wholes are equal.)
⇒ 2AP = AB ——— (i)
Similarly,
2 AQ = AB ——— (ii)
From (i) and (ii), Since R.H.S are same, we equate the L.H.S
2 AP = 2 AQ (Things which are equal to the same thing are equal to one another.)
⇒ AP = AQ (Things which are double of the same things are equal to one another.)
Thus, we conclude that P and Q are the same points.
This contradicts our assumption that P and Q are two different mid points of AB.
Thus, it is proved that every line segment has one and only one mid-point.
Hence Proved.
6. In Fig. 5.10, if AC = BD, then prove that AB = CD.
Answer –
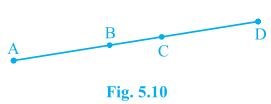
It is given, AC = BD
From the given figure, we get,
AC = AB+BC
BD = BC+CD
⇒ AB+BC = BC+CD [AC = BD, given]
We know that, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S and R.H.S of the equation AB+BC = BC+CD, we get,
AB + BC – BC = BC + CD – BC
AB = CD
Hence Proved.
7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Answer – Axiom 5 of Euclid’s Axioms states that – “The whole is greater than the part.” This axiom is known as a universal truth because it holds true in any field of mathematics and in other disciplinarians of science as well. AB is a whole part.
