NCERT Solutions Class 9 Maths
Chapter – 15 (Probability)
The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 15 Probability Exercise 15.1 has been provided here to help the students in solving the questions from this exercise.
Exercise – 15.1
1. In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Answer –
Number of balls played = 30
Number of balls for which the batswoman hits boundary = 6
Thus, number of balls for which the batswoman does not hit a boundary = 30 – 6 = 24
Probability, P(E) = Number of instances of the event taking place / Total number of instances.
= 24/30
= 4/5
2. 1500 families with 2 children were selected randomly, and the following data were recorded:
| Number of girls in a family | 2 | 1 | 0 |
| Number of families | 475 | 814 | 211 |
Compute the probability of a family, chosen at random, having
(i) 2 girls
(ii) 1 girl
(iii) No girl
Also check whether the sum of these probabilities is 1.
Answer –
Total number of families = 1500
(i) Number of families having 2 girls, P(2)= 475
Probability = Number of families having 2 girls/Total number of families
= 475/1500
= 19/60
(ii) Number of families having 1 girl, P(1) = 814
Probability = Number of families having 1 girl/Total number of families
= 814/1500
= 407/750
(iii) Number of families having 0 girls, P(0)= 211
Probability = Number of families having 0 girls/Total number of families
= 211/1500
Now, sum of all the three probabilities = P(2) + P(1) + P(0)
= 475/1500 + 814/1500 + 211/1500
= (475 + 814 + 211) / 1500
= 1500/1500
= 1
Yes, the sum of these probabilities is 1.
3. Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.
Answer –
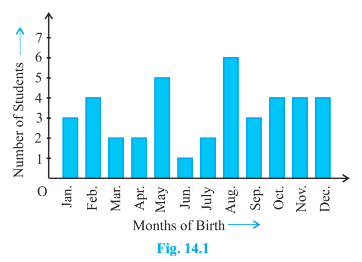
Total number of students in the class = 40
Number of students born in August = 6
Probability of students born in August = Number of students born in August / Total number of students in class
= 6/40
= 3/20
4. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:
| Outcome | 3 heads | 2 heads | 1 head | No head |
| Frequency | 23 | 72 | 77 | 28 |
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Answer –
Number of times 2 heads come up = 72
Total number of times the coins were tossed = 200
Probability of 2 heads outcomes = Number of 2 heads outcomes / Total number of tosses
= 72/200
= 9/25
5. An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
| Monthly income (in ₹) |
Vehicles per family | |||
| 0 | 1 | 2 | Above 2 | |
| Less than 7000 | 10 | 160 | 25 | 0 |
| 7000-10000 | 0 | 305 | 27 | 2 |
| 10000-13000 | 1 | 535 | 29 | 1 |
| 13000-16000 | 2 | 469 | 59 | 25 |
| 16000 or more | 1 | 579 | 82 | 88 |
Suppose a family is chosen. Find the probability that the family chosen is
(i) earning ₹10000 – 13000 per month and owning exactly 2 vehicles.
(ii) earning ₹16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than ₹7000 per month and does not own any vehicle.
(iv) earning ₹13000 – 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Answer – Total number of families = 2400
(i) Number of families earning ₹10000 –13000 per month and owning exactly 2 vehicles = 29
Probability of family earning ₹ 10000 – 13000 per month and owning exactly 2 vehicles = 29/2400
(ii) Number of families earning ₹16000 or more per month and owning exactly 1 vehicle = 579
Probability of family earning ₹ 16000 or more per month and owning exactly 1 vehicle = 579/2400
(iii) Number of families earning less than ₹7000 per month and does not own any vehicle = 10
Probability of family earning less than ₹ 7000 per month and does not own any vehicle = 10/2400 = 1/240
(iv) Number of families earning ₹13000-16000 per month and owning more than 2 vehicles = 25
Probability of family earning ₹ 13000 – 16000 per month and owning more than 2 vehicles = 25/2400 = 1/96
(v) Number of families owning not more than 1 vehicle = 10 + 160 + 0 + 305 + 1 + 535 + 2 + 469 + 1 + 579 = 2062
Probability of family owning not more than 1 vehicle = 2062/2400 = 1031/1200
6. Refer to Table 14.7, Chapter 14.
(i) Find the probability that a student obtained less than 20% in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.
Answer –
| Marks | Number of students |
| 0 – 20 | 7 |
| 20 – 30 | 10 |
| 30 – 40 | 10 |
| 40 – 50 | 20 |
| 50 – 60 | 20 |
| 60 – 70 | 15 |
| 70 – above | 8 |
| Total | 90 |
Total number of students = 90
(i) Number of students that obtained less than 20% marks = 7
Probability of students that obtained less than 20% marks = 7/90
(ii) Number of students that obtained 60 marks or above = 15 + 8 = 23
Probability of students that obtained 60 marks or above = 23/90
7. To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.
| Opinion | Number of students |
| like | 135 |
| dislike | 65 |
Find the probability that a student chosen at random
(i) likes statistics,
(ii) does not like it.
Answer –
Total number of students = 135+65 = 200
(i) Number of students who like statistics = 135
Probability of students who like statistics = 135/200 = 27/40
(ii) Number of students who do not like statistics = 65
Probability of students who dislike statistics = 65/200 = 13/40
8. Refer to Q.2, Exercise 14.2. What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work?
(iii) Within ½ km from her place of work?
Answer – The distance (in km) of 40 engineers from their residence to their place of work were found as follows:
| 5 | 3 | 10 | 20 | 25 | 11 | 13 | 7 | 12 | 31 |
| 19 | 10 | 12 | 17 | 18 | 11 | 32 | 17 | 16 | 2 |
| 7 | 9 | 7 | 8 | 3 | 5 | 12 | 15 | 18 | 3 |
| 12 | 14 | 2 | 9 | 6 | 15 | 15 | 7 | 6 | 12 |
Total numbers of engineers = 40
(i) Number of engineers living less than 7 km from their place of work = 9
Probability of an engineer who lives less than 7 km from their place of work = 9/40
(ii) Number of engineers living more than or equal to 7 km from their place of work = 40 – 9 = 31
Probability of an engineer who lives more than or equal to 7 km from their place of work = 31/40
(iii) Number of engineers living within ½ km from their place of work = 0
Probability of an engineer who lives within 1/2 km from their place of work = 0/40 = 0
9. Activity : Note the frequency of two-wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Answer – The question is an activity to be performed by the students.
Hence, perform the activity by yourself and note down your inference.
10. Activity : Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.
Answer – The question is an activity to be performed by the students.
Hence, perform the activity by yourself and note down your inference.
11. Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Answer – Total number of bags present = 11
Number of bags containing more than 5 kg of flour = 7
Probability of a bag containing more than 5 kg of flour = 7/11
12. In Q.5, Exercise 14.2, you were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12-0.16 on any of these days.The data obtained for 30 days is as follows:
| 0.03 | 0.08 | 0.08 | 0.09 | 0.04 | 0.17 |
| 0.16 | 0.05 | 0.02 | 0.06 | 0.18 | 0.20 |
| 0.11 | 0.08 | 0.12 | 0.13 | 0.22 | 0.07 |
| 0.08 | 0.01 | 0.10 | 0.06 | 0.09 | 0.18 |
| 0.11 | 0.07 | 0.05 | 0.07 | 0.01 | 0.04 |
Answer –
Total number of days in which the data was recorded = 30 days
Number of days in which sulphur dioxide was present in between the interval 0.12 – 0.16 = 2
Probability of the concentration of Sulphur dioxide in the interval 0.12 – 0.16 = 2/30 = 1/15
13. In Q.1, Exercise 14.2, you were asked to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB. The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Answer –
Total numbers of students = 30
Number of students having blood group AB = 3
Probability of students having blood group AB = (Number of students having blood group AB) / Total number of students = 3/30 = 1/10

Leave a Reply