NCERT Solutions Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4

NCERT Solutions Class 9 Maths
Chapter – 13 (Surface Areas and Volumes)

The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 13 Surface Areas and Volumes Exercise 13.4 has been provided here to help the students in solving the questions from this exercise.

Chapter 13: Surface Areas and Volumes

Exercise – 13.4

1. Find the surface area of a sphere of radius:
(i) 10.5cm
(ii) 5.6cm
(iii) 14cm
(Assume π = $\mathbf{\frac{22}{7}}$ )

Answer –

(i) Radius of the sphere, r = 10.5 cm
Surface area of the sphere = 4πr²= 4 × $\frac{22}{7}$ × 10.5 cm²= 1386 cm²Surface area of the sphere is 1386 cm²

(ii) Radius of the sphere, r = 5.6cm
Surface area of the sphere = 4πr²= 4 × $\frac{22}{7}$ × 5.6 cm²= 394.24 cm²

(iii) Radius, r = 14 cm
Surface area of the sphere = 4πr²= 4 × $\frac{22}{7}$ × 14 cm²= 2464 cm²

2. Find the surface area of a sphere of diameter:
(i) 14 cm
(ii) 21 cm
(iii) 3.5 cm
(Assume π = $\mathbf{\frac{22}{7}}$ )

Answer –

(i) Radius of sphere, r = diameter/2 = 14/2 cm = 7 cm
Surface area of a sphere = 4πr²= 4 × $\frac{22}{7}$ × 7cm × 7cm
= 616 cm²Surface area of the sphere is 616 cm²

(ii) Radius of the sphere, r = diameter/2 = 21/2 = 10.5 cm
Surface area of a sphere = 4πr²= 4 × $\frac{22}{7}$ × 10.5²= 1386
Surface area of the sphere is 1386 cm²

(iii) Radius of sphere, r = diameter/2 = 3.5/2 = 1.75 cm
Surface area of a sphere = 4πr²= 4 × $\frac{22}{7}$ × 1.75²
= 38.5
Surface area of the sphere is 38.5 cm²

3. Find the total surface area of a hemisphere of radius 10 cm. [Use π=3.14]

Answer –
Radius of the hemisphere, r = 10 cm
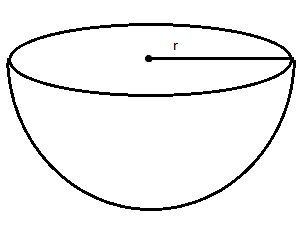
NCERT Class 9 Solutions Maths
The total surface area of a hemisphere = (4πr²)/2 + πr² = 3πr²= 3 × 3.14 × 10²
= 942
The total surface area of the given hemisphere is 942 cm².

4. The radius of a spherical balloon increases from 7cm to 14cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.

Answer –
The radius of the balloon before pumping air, r_₁ = 7cm
The radius of the balloon after pumping air, r_₂ = 14cm
The surface area of the balloon before pumping air, SA_₁ = 4π(r_₁)²The surface area of the balloon after pumping air, SA_₂ = 4π(r_₂)²The ratio of the surface areas of the balloon, = SA_₁/CSA_₂= 4π(r_₁)²/4π(r_₂)²= (r_₁)²/(r_₂)²= (r_₁/r_₂)²= (7/14)²= (1/2)²= (1/4)
The ratio of the surface areas of the balloons = 1: 4

5. A hemispherical bowl made of brass has inner diameter 10.5cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm². (Assume π = $\mathbf{\frac{22}{7}}$ )

Answer –
Inner diameter, d = 10.5 cm
Inner radius, r = d/2 = 10.5/2cm = 5.25 cm
CSA of hemispherical bowl = 2πr²= 2 × $\frac{22}{7}$ × 5.25 cm × 5.25 cm
= 173.25 cm²The cost of tin-plating 100 cm² of the bowl = ₹16
The cost of tin-plating 1 cm² of the bowl = ₹16/100
The cost of tin-plating 173.25 cm²area of the bowl = (₹16/100) × 173.25 = 27.72
Thus, the cost of tin-plating is ₹ 27.72.

6. Find the radius of a sphere whose surface area is 154 cm². (Assume π = $\mathbf{\frac{22}{7}}$ )
Answer – Let the radius of the sphere = r
The surface area of the sphere = 154 cm²4πr² = 154 cm²r² = $\frac{154}{4\Pi}$

r² = $\frac{154}{4\times \frac{22}{7}}$

r² = $\frac{154\times 7}{4\times 22}$

r² = $\frac{49}{4}$

r = $\frac{7}{2}$ = 3.5 cm
Thus, the radius of the sphere whose surface area is 154 cm² is 3.5 cm.

7. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.

Answer –
Let the radius of the earth = R
the radius of the moon = r
Diameter of the moon = 1/4 × diameter of the earth
Thus, the radius of the moon = 1/4 × radius of the earth [Since, radius = 2 × Diameter]
r = 1/4 × R
r/R = 1/4 ———— (1)
Now, the surface area of earth = 4πR²The surface area of moon = 4πr²The ratio of their surface areas = 4πr²/4πR²= r²/R²= (r/R)²= (1/4)² [From equation (1)]
= 1/16
The ratio of their surface areas = 1 : 16

8. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5cm. Find the outer curved surface of the bowl. (Assume π = $\mathbf{\frac{22}{7}}$ )

Answer – The inner radius of the bowl, r = 5 cm
Thickness of steel = 0.25 cm
Outer radius of the bowl, R = 5 cm + 0.25 cm = 5.25 cm
Outer CSA of the hemisphere = 2πR²= 2 × $\frac{22}{7}$ × 5.25 cm × 5.25 cm
= 173.25 cm²Thus, the outer curved surface area of the hemisphere is 173.25 cm².

9. A right circular cylinder just encloses a sphere of radius r (see fig. 13.22). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in(i) and (ii).

Answer –
The radius of the sphere = Radius of the cylinder = r
Height of the cylinder, h = diameter of the sphere = 2r
Thus, h = 2r

(i) Surface area of sphere = 4πr²

(ii) Height of cylinder, h = r + r = 2r
Radius of cylinder = r
CSA of cylinder formula = 2πrh = = 2πr × 2r
= 4πr²

(iii) Ratio between areas = (Surface area of sphere)/(CSA of Cylinder)
= 4πr²/4πr²= 1/1

Thus, the surface area of the sphere and the curved surface area of the cylinder is 4πr² and the ratio between these areas is 1 : 1.

NCERT Solutions Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4