NCERT Solutions Class 9 Maths Chapter 10 Circles Ex 10.6

NCERT Solutions Class 9 Maths
Chapter – 10 (Circles)

The NCERT Solutions in English Language for Class 9 Mathematics Chapter – 10 Circles Exercise 10.6 has been provided here to help the students in solving the questions from this exercise.

Chapter 10: Circles

Exercise – 10.6

1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Answer – Consider the following diagram
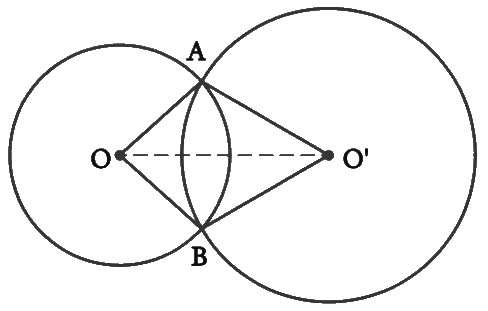
NCERT Class 9 Solutions Maths
We need to prove that ∠OAO’= ∠OBO’
Consider ΔOAO’ and ΔOBO’
OA = OB (Radii of a circle with center O)
O’A = O’B (Radii of a circle with center O’)
OO’= OO’ (Common)
Therefore, by SSS criteria, ΔOAO’ and ΔOBO’ are congruent to each other.
By CPCT, ∠OAO’= ∠OBO’
Hence it is proved that the line of centers of two intersecting circles subtends equal angles at the two points of intersection.

2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 , find the radius of the circle.
Answer – Draw two parallel chords AB and CD of lengths 5 cm and 11 cm. Let the center of the circle be O. Join one end of each chord to the center.

Thus, MB = 2.5 cm and ND = 5.5 cm [The perpendicular drawn from the center of the circle to the chords bisects it.]
Let OM = x and ON = 6 – x
Consider ΔOMB
By Pythagoras theorem,
OM² + MB² = OB²x² + 2.5² = OB²x² + 6.25 = OB²———————–(1)
Consider ΔOND
By Pythagoras theorem,
ON² + ND² = OD²(6 – x)² + 5.5² = OD²36 + x² – 12x + 30.25 = OD²x² – 12x + 66.25 = OD²———————–(2)
OB and OD are the radii of the circle. Therefore OB = OD.
Thus, OB² = OD²Equating (1) and (2) we get,
x² + 6.25 = x² – 12x + 66.25
12x = 60
x = 5
Substituting the value of x in (1),
OB² = x² + 6.25
OB² = 5²+ 6.25
OB² = 31.25
OB = 5.59 (approx.)
Thus, we get the radius of the circle = 5.59 cm.

3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance 4 cm from the centre, what is the distance of the other chord from the centre?
Answer – Consider the following diagram
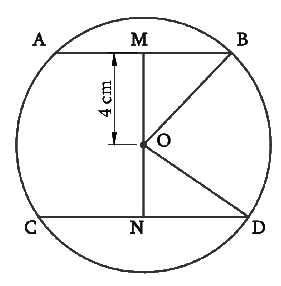
NCERT Class 9 Solutions Maths
AB = 6 cm CD = 8 cm MB = 3 cm ND = 4 cm
Given OM = 4 cm and let ON = x cm Consider ΔOMB
By Pythagoras theorem,
OM² + MB² = OB²
4² + 3² = OB²
OB² = 25
OB = 5 cm
OB and OD are the radii of the circle.
Therefore OD = OB = 5 cm.
Consider ΔOND
By Pythagoras theorem,
ON² + ND² = OD²
x² + 4² = 5²
x² = 25 – 16
x² = 9
x = 3
The distance of the chord CD from the center is 3 cm.

4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Answer – Consider the diagram
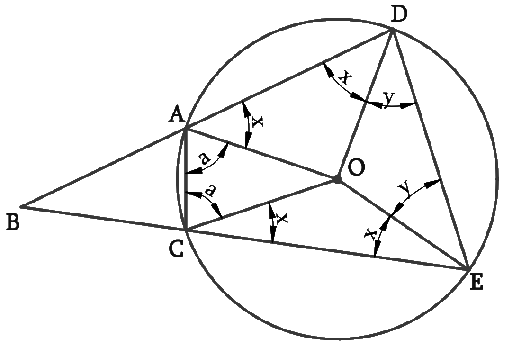
NCERT Class 9 Solutions Maths
To prove: ∠ABC = $\frac{1}{2}$ (∠DOE – ∠AOC)
Consider ΔAOD and ΔCOE,
OA = OC (Radii of the circle)
OD = OE (Radii of the circle)
AD = CE (Given)
Thus, ∆AOD ≅ ∆COE (SSS Congruence Rule)
∠OAD = ∠OCE (By CPCT) ———– (1)
∠ODA = ∠OEC (By CPCT) ———– (2)
Also,
∠OAD = ∠ODA (As OA = OD) ———– (3)
From Equations (1), (2), and (3), we obtain
∠OAD = ∠OCE = ∠ODA = ∠OEC
Let ∠OAD = ∠OCE = ∠ODA = ∠OEC = x
In ΔOAC,
OA = OC
∴ ∠OCA = ∠OAC (Angle a)
In ΔODE,
OD = OE
∠OED = ∠ODE (Angle y)
ADEC is a cyclic quadrilateral.
∴ ∠CAD + ∠DEC = 180° (Opposite angles are supplementary)
x + a + x + y = 180°
2x + a + y = 180°
y = 180° – 2x – a ———– (4)
However, ∠DOE = 180° – 2y and, ∠AOC = 180° − 2a
∠DOE – ∠AOC = 2a – 2y
= 2a – 2 (180° – 2x – a) [From equation (4)]
= 4a + 4x – 360° ———– (5)
∠BAC + ∠CAD = 180° (Linear pair)
∴ ∠BAC = 180º – ∠CAD = 180° – (a + x) ———– (6)
Similarly, ∠ACB = 180° – (a + x) ———– (7)
In ΔABC,
∠ABC + ∠BAC + ∠ACB = 180° (Angle sum property of a triangle)
∠ABC = 180° – ∠BAC – ∠ACB
= 180° – (180° – a – x) – (180° – a – x) [From (6) and (7)]
= 2a + 2x -180°
= $\frac{1}{2}$ [4a + 4x – 360°]
Using Equation (5)
∠ABC = $\frac{1}{2}$ (∠DOE – ∠AOC)
Hence it is proved that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the center

5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Answer – Consider the diagram
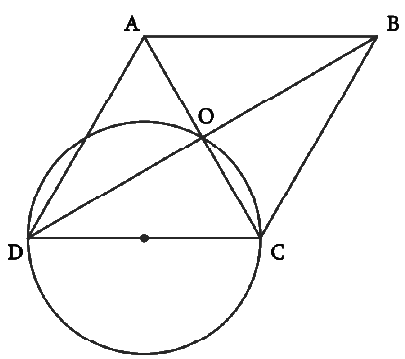
NCERT Class 9 Solutions Maths
Let ABCD be a rhombus in which diagonals intersect at point O, and a circle is drawn by taking side CD as its diameter. We know that a diameter subtends 90° on the arc.
Therefore, ∠COD = 90°
Also, in the rhombus, the diagonals intersect each other at 90°.
∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
But ∠COD is 90° and this can only happen on a semicircle with diameter DC since the angle subtended by the diameter on a semicircle is 90°.
Clearly, point O has to lie on the circle.
Thus, the circle passes through the point of intersection of its diagonals O.

6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE, = AD.
Answer – Consider the diagram
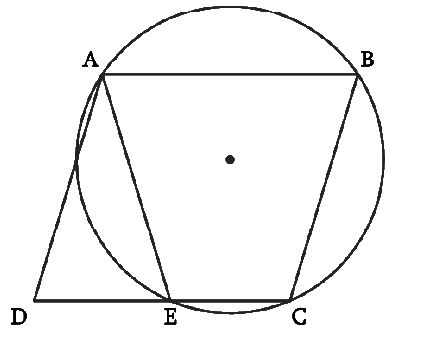
NCERT Class 9 Solutions Maths
We can see that ABCE is a cyclic quadrilateral.
We know that in a cyclic quadrilateral, the sum of the opposite angles is 180°.
∠AEC + ∠CBA = 180°
∠AEC + ∠AED = 180° (Linear pair)
Thus, ∠AED = ∠CBA ————– (1)
We know that in a parallelogram, opposite angles are equal.
∠ADE = ∠CBA ————– (2)
From (1) and (2),
∠AED = ∠ADE
Therefore, AD = AE (sides opposite to equal angles in a triangle are equal).
Hence proved.

7. AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters;
(ii) ABCD is a rectangle.
Answer – Consider the diagram
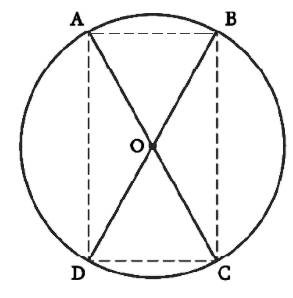
NCERT Class 9 Solutions Maths
Let AC and BD be two chords intersecting at O.
In ΔAOB and ΔCOD,
OA = OC (Given)
OB = OD (Given)
∠AOB = ∠COD (Vertically opposite angles)
Hence, ΔAOB ≅ ΔCOD (SAS congruence rule)
AB = CD (By CPCT)
Similarly, it can be proved that ΔAOD ≅ ΔCOB
Hence, AD = CB (By CPCT)
Since in quadrilateral ABCD, opposite sides are equal in length, ABCD is a parallelogram.
We know that opposite angles of a parallelogram are equal.
Therefore, ∠A = ∠C
However, ∠A + ∠C = 180° (ABCD is a cyclic quadrilateral)
∠A + ∠A = 180°
2∠A = 180°
∴ ∠A = 90°
ABCD is a parallelogram and one of its interior angles is 90°, therefore, it is a rectangle.
∠A is the angle subtended by chord BD, ∠A = 90°, therefore, BD should be the diameter of the circle [Since, angle in a semicircle is a right angle]
Similarly, AC is the diameter of the circle.
Thus, (i) AC and BD are diameters, and (ii) ABCD is a rectangle, proved

8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90°–(½)A, 90°–(½)B and 90°–(½)C.
Answer – Consider the following diagram
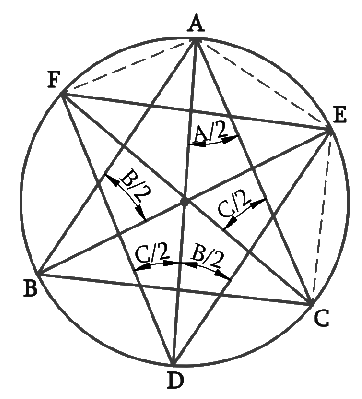
NCERT Class 9 Solutions Maths
A diagram is constructed as per the given question.
It is given that BE is the bisector of ∠B, AD is the bisector of ∠A and CF is the bisector of ∠C.
Thus, ∠ABE = $\frac{\angle B}{2}$
However, ∠ADE = ∠ABE (Angles in the same segment for chord AE)
Thus, ∠ADE = $\frac{\angle B}{2}$
Similarly, ∠ADF = ∠ACF = ∠C/2 (Angle in the same segment for chord AF)
∠D = ∠ADE + ∠ADF
= $\frac{\angle B}{2}$ + $\frac{\angle C}{2}$ [Since ∠ADE = $\frac{\angle B}{2}$ and ∠ADF = $\frac{\angle C}{2}$ ]

= $\frac{1}{2}$ (∠B + ∠C )

= $\frac{1}{2}$ (180° – ∠A) [Angle sum property of triangle ABC]
= 90° – $\frac{1}{2}$ A
Similarly, it can be proved for
∠E = 90° – $\frac{1}{2}$ B

∠F = 90° – $\frac{1}{2}$ C.
Thus we have proved that the angles of the triangle DEF are 90° – $\frac{1}{2}$ A, 90° – $\frac{1}{2}$ B, 90° – $\frac{1}{2}$ C.

9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Answer – Consider the diagram
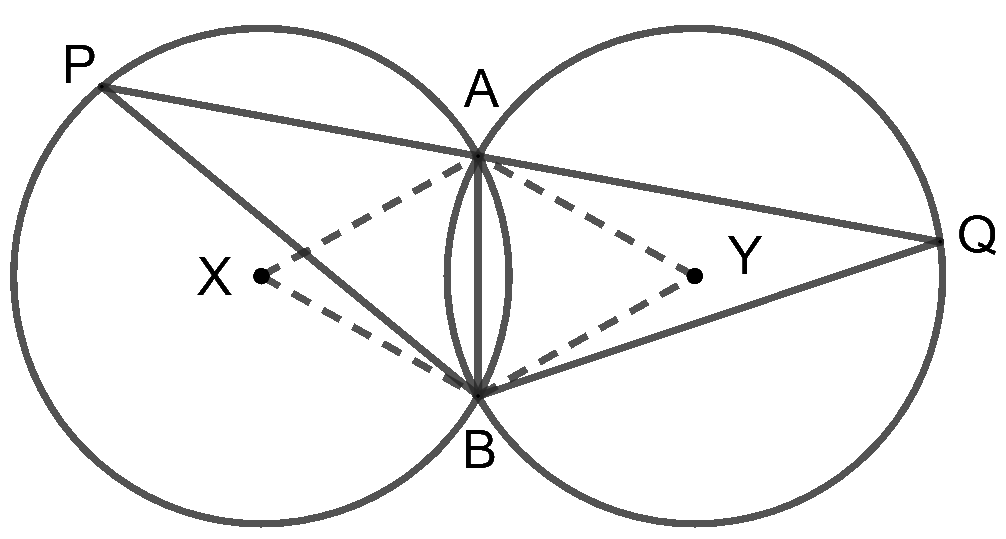
NCERT Class 9 Solutions Maths
AB is the common chord to both circles.
Since the circles are congruent, their radii are equal.
In triangles ABX and ABY
AB = AB (Common)
AX = AY (equal radii)
BX = BY (equal radii)
By SSS congruence criteria, triangles ABX and ABY are congruent.
Hence ∠X = ∠Y [CPCT] ————- (1)
Now, we know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle
Thus,
∠APB = $\frac{1}{2}$ ∠X ————- (2)

∠AQB = $\frac{1}{2}$ ∠Y ————- (3)
Therefore,
∠APB = ∠AQB [From equations (1), (2) and (3)]
Consider the ΔBPQ,
∠APB = ∠AQB
This implies that ΔBPQ is an isosceles triangle as base angles are equal.
Therefore, we get BP = BQ, sides opposite to equal sides in a triangle are equal.

10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Answer – Consider the diagram
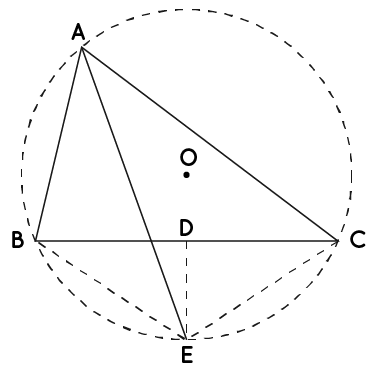
NCERT Class 9 Solutions Maths

Let AE be the angle bisector of ∠A.
We need to prove that ED is the perpendicular bisector of BC.
∠BAE = ∠CAE ————- (1) [Since, AE is the angle bisector of ∠A]
Now, ∠EBC = ∠CAE ————- (2) [Angles subtended by the same arc EC]
Also, ∠ECB = ∠BAE ————- (3) [Angles subtended by the same arc BE]
But we know that, ∠BAE = ∠CAE [From equation (1)]
Hence, ∠EBC = ∠ECB [From equations (2) and (3)]
Therefore, BE = EC [Sides opposite to equal angles are equal]
Thus, point E is equidistant from the points B and C. This is only possible when E lies on the perpendicular bisector of BC.
Thus, ED is the perpendicular bisector of BC.
Therefore, the perpendicular bisector of side BC and the angle bisector of ∠A meet on the circumcircle of triangle ABC at point E.

NCERT Solutions Class 9 Maths Chapter 10 Circles Ex 10.6