NCERT Solutions Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1

NCERT Solutions Class 8 Mathematics 
Chapter – 7 (Cubes and Cube Roots) 

The NCERT Solutions in English Language for Class 8 Mathematics Chapter – 7 Cubes and Cube Roots Exercise 7.1 has been provided here to help the students in solving the questions from this exercise. 

Chapter 7: Cubes and Cube Roots

• NCERT Solution Class 8 Maths Ex – 7.2

Exercise – 7.1 

1. Which of the following numbers are not perfect cubes?
(i) 216                       (ii) 128                           (iii) 1000
(iv) 100                    (v) 46656

Solution –
(i) 216

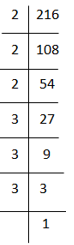
216 = 2 × 2 × 2 × 3 × 3 × 3
= (2×2×2) × (3×3×3)
= (2×3)³
= 6³
Hence, = 6

(ii) 128

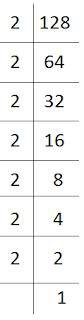
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
= (2×2×2) × (2×2×2) × 2
Here, 128 cannot be grouped into triplets of equal factors, and we are left with one factor: 2.
∴ 128 is not a perfect cube.

(iii) 1000

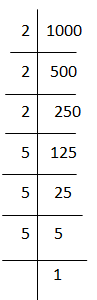
1000 = 2 × 2 × 2 × 5 × 5 × 5
= (2×2×2) × (5×5×5)
= (2×5)³
= 103
Hence, = 10.

(iv) 100

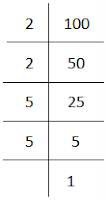
100 = 2 × 2 × 5 × 5
Here, 100 cannot be grouped into triplets of equal factors.
∴ 100 is not a perfect cube.

(v) 46656

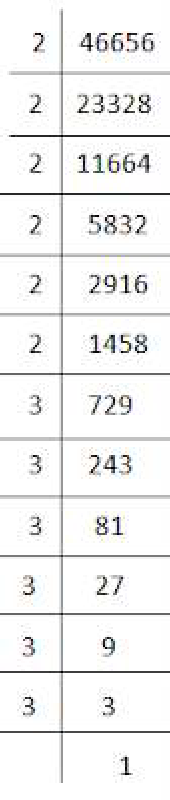
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
= (2×2×2) × (2×2×2) × (3×3×3) × (3×3×3)
= (2×2×3×3)³
= 36³
Hence, = 36.

2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243                          (ii) 256                        (iii) 72
(iv) 675                        (v) 100

Solution –
(i) 243

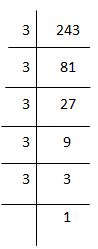
243 = 3 × 3 × 3 × 3 × 3
= (3×3×3) × 3×3
Here, 3 cannot be grouped into triplets of equal factors.
∴ We will multiply 243 by 3 to get the perfect cube.

(ii) 256

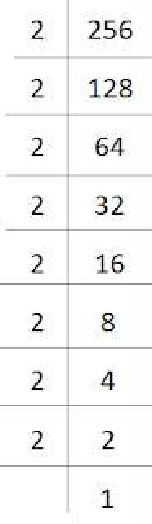
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= (2×2×2) × (2×2×2) × 2 × 2
Here, 2 cannot be grouped into triplets of equal factors.
∴ We will multiply 256 by 2 to get the perfect cube.

(iii) 72

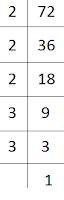
72 = 2 × 2 × 2 × 3 × 3
= (2×2×2) × 3 × 3
Here, 3 cannot be grouped into triplets of equal factors.
∴ We will multiply 72 by 3 to get the perfect cube.

(iv) 675

675 = 3 × 3 × 3 × 5 × 5
= (3×3×3) × 5 × 5
Here, 5 cannot be grouped into triplets of equal factors.
∴ We will multiply 675 by 5 to get the perfect cube.

(v) 100

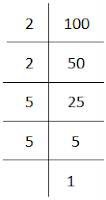
100 = 2 × 2 × 5 × 5
Here, 2 and 5 cannot be grouped into triplets of equal factors.
∴ We will multiply 100 by (2×5) 10 to get the perfect cube.

3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704

Solution –
(i) 81

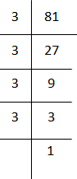
81 = 3 × 3 × 3 × 3
= (3×3×3) × 3
Here, 3 cannot be grouped into triplets of equal factors.
∴ We will divide 81 by 3 to get the perfect cube.

(ii) 128

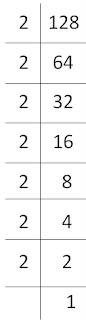
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
= (2×2×2) × (2×2×2) × 2
Here, 2 cannot be grouped into triplets of equal factors.
∴ We will divide 128 by 2 to get the perfect cube.

(iii) 135

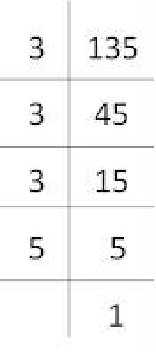
135 = 3 × 3 × 3 × 5
= (3×3×3) × 5
Here, 5 cannot be grouped into triplets of equal factors.
∴ We will divide 135 by 5 to get the perfect cube.

(iv) 192

192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
= (2×2×2) × (2×2×2) × 3
Here, 3 cannot be grouped into triplets of equal factors.
∴ We will divide 192 by 3 to get the perfect cube.

(v) 704

704 = 2 × 2 × 2 × 2 × 2 × 2 × 11
= (2×2×2) × (2×2×2) × 11
Here, 11 cannot be grouped into triplets of equal factors.
∴ We will divide 704 by 11 to get the perfect cube.

4. Parikshit makes a cuboid of plasticine with sides 5 cm, 2 cm, and 5 cm. How many such cuboids will he need to form a cube?

Solution – Given the sides of the cube are 5 cm, 2 cm and 5 cm.
∴ Volume of cube = 5×2×5 = 50 cm³
Here, 2, 5 and 5 cannot be grouped into triplets of equal factors.
∴ We will multiply 50 by (2×2×5) 20 to get the perfect cube.
Hence, 20 cuboids are needed.