NCERT Solutions Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3

NCERT Solutions Class 8 Mathematics 
Chapter – 6 (Squares and Square) 

The NCERT Solutions in English Language for Class 8 Mathematics Chapter – 6 Squares and Square Exercise 6.3 has been provided here to help the students in solving the questions from this exercise. 

Chapter 6: Squares and Square Roots

• NCERT Solution Class 8 Maths Ex – 6.1
• NCERT Solution Class 8 Maths Ex – 6.2
• NCERT Solution Class 8 Maths Ex – 6.4

Exercise – 6.3 

1. What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025

Solution –
(i) 9801
1 x 1 = 1 and 9 x 9 = 81
∵ The possible one’s digit of the square root of the number 9801 could be 1 or 9.

(ii) 99856
4 x 4 = 16 and 6 x 6 = 36
∵ The possible one’s digit of the square root of the number 99856 could be 4 or 6.

(iii) 998001
1 × 1 = 1 and 9 x 9 = 81
∵ The possible one’s digit of the square root of the number 998001 could be 1 or 9.

(iv) 657666025
5 x 5 = 25
∵ The possible one’s digit of the square root of the number 657666025 could be 5.

2. Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153
(ii) 257
(iii) 408
(iv) 441

Solution – We know that natural numbers ending with the digits 0, 2, 3, 7 and 8 are not perfect square.

(i) 153
The number 153 is surely not a perfect square because it ends in 3 whereas the square numbers end with 0, 1, 4, 5, 6 or 9.

(ii) 257
The number 257 is surely not a perfect square because it ends in 7 whereas the square numbers end with 0, 1, 4, 5, 6 or 9.

(iii) 408
The number 408 is surely not a perfect square because it ends in 8 whereas the square numbers end with 0, 1, 4, 5, 6 or 9.

(iv) 441
The number may be a perfect square as the square numbers end wTith 0, 1, 4, 5, 6 or 9.

3. Find the square roots of 100 and 169 by the method of repeated subtraction.

Solution –
100
100 – 1 = 99
99 – 3 = 96
96 – 5 = 91
91 – 7 = 84
84 – 9 = 75
75 – 11 = 64
64 – 13 = 51
51 – 15 = 36
36 – 17 = 19
19 – 19 = 0
Here, we have performed subtraction ten times.
∴ √100 = 10

169
169 – 1 = 168
168 – 3 = 165
165 – 5 = 160
160 – 7 = 153
153 – 9 = 144
144 – 11 = 133
133 – 13 = 120
120 – 15 = 105
105 – 17 = 88
88 – 19 = 69
69 – 21 = 48
48 – 23 = 25
25 – 25 = 0
Here, we have performed subtraction thirteen times.
∴ √169 = 13

4. Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729                       (ii) 400                             (iii) 1764
(iv) 4095                  (v) 7744                            (vi) 9604
(vii) 5929                 (viii) 9216                       (ix) 529
(x) 8100

Solution –

(i) 729

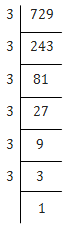
729 = 3 × 3 × 3 × 3 × 3 × 3
⇒ 729 = (3×3)×(3×3)×(3×3)
⇒ 729 = (3)³
⇒ √729 = 3×3×3 = 27

(ii) 400       

400 = 2 × 2 × 2 × 2 × 5 × 5
⇒ 400 = (2×2)×(2×2)×(5×5)
⇒ 400 = (2×2×5)² =20²
⇒ √400 = 20

(iii) 1764

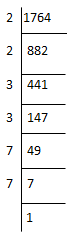
1764 = 2 × 2 × 3 × 3 × 7 × 7
⇒ 1764 = (2×2)×(3×3)×(7×7)
⇒ 1764 = (2×3×7)² = 42²
⇒ √1764 = 42

(iv) 4096

4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
⇒ 4096 = (2×2)×(2×2)×(2×2)×(2×2)×(2×2)×(2×2)
⇒ 4096 = (2×2×2×2×2×2)² = 64²
⇒ √4096 = 64

(v) 7744

7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
⇒ 7744 = (2×2)×(2×2)×(2×2)×(11×11)
⇒ 7744 = (2×2×2×11)² = 88²
⇒ √7744 = 88

(vi) 9604

9604 = 2 × 2 × 7 × 7 × 7 × 7
⇒ 9604 = ( 2 × 2 ) × ( 7 × 7 ) × ( 7 × 7 )
⇒ 9604 = ( 2×7×7 )² = 98²
⇒ √9604 = 98

(vii) 5929

5929 = 7 × 7 × 11 × 11
⇒ 5929 = (7×7)×(11×11)
⇒ 5929 = (7×11)² = 77²
⇒ √5929 = 77

(viii) 9216

9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
⇒ 9216 = (2×2) × (2×2) × ( 2 × 2 ) × ( 2 × 2 ) × ( 2 × 2 ) × ( 3 × 3 )
⇒ 9216 = 96 × 96
⇒ 9216 = (96)²
⇒ √9216 = 96

(ix) 529

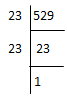
529 = 23 × 23
529 = (23)²
√529 = 23

(x) 8100

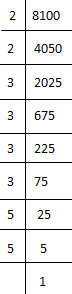
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
⇒ 8100 = (2×2) ×(3×3)×(3×3)×(5×5)
⇒ 8100 = (2×3×3×5)×(2×3×3×5)
⇒ 8100 = 90×90
⇒ 8100 = (90)²
⇒ √8100 = 90

5. For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768

Solution –

(i) 252

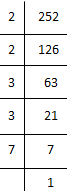
252 = 2 × 2 × 3 × 3 × 7
= (2×2) × (3×3) × 7
Here, 7 cannot be paired.
∴ We will multiply 252 by 7 to get perfect square.
New number = 252 × 7 = 1764
Now each prime factor has a pair. Therefore, 252 × 7 = 1764 is a perfect square.
Thus the required smallest number is 7.
⇒ √1764 = 2 × 3 × 7 = 42

(ii) 180

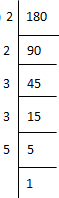
180 = 2 × 2 × 3 × 3 × 5
= (2×2) × (3×3) × 5
Here, 5 cannot be paired.
∴ We will multiply 180 by 5 to get perfect square.
New number = 180 × 5 = 900
Now each prime factor has a pair. Therefore, 180 × 5 = 900 is a perfect square.
Thus the required smallest number is 5.
⇒ √900 = 2×3×5 = 30

(iii) 1008

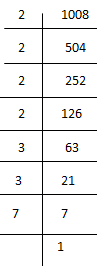
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
= (2×2) × (2×2) × (3×3) × 7
Here, 7 cannot be paired.
∴ We will multiply 1008 by 7 to get perfect square.
New number = 1008 × 7 = 7056
Now each prime factor has a pair. Therefore, 1008 × 7 = 7056 is a perfect square.
Thus the required smallest number is 7.
⇒ √7056 = 2×2×3×7 = 84

(iv) 2028

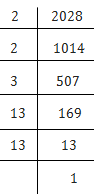
2028 = 2 × 2 × 3 × 13 × 13
= (2×2) × (13×13) × 3
Here, 3 cannot be paired.
∴ We will multiply 2028 by 3 to get perfect square.
New number = 2028 × 3 = 6084
Now each prime factor has a pair. Therefore, 2028 × 3 = 6084 is a perfect square.
Thus the required smallest number is 3.
⇒ √6084 = 2 × 3 × 13 = 78

(v) 1458

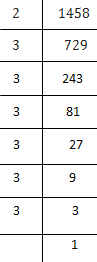
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
= (3×3) × (3×3) × (3×3) × 2
Here, 2 cannot be paired.
∴ We will multiply 1458 by 2 to get perfect square.
New number = 1458 × 2 = 2916
Now each prime factor has a pair. Therefore, 1458 × 2 = 2916 is a perfect square.
Thus the required smallest number is 2.
⇒ √2916 = 3×3×3×2 = 54

(vi) 768

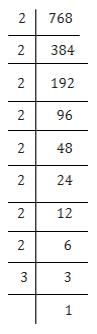
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
= (2×2) × (2×2) × (2×2) × (2×2) × 3
Here, 3 cannot be paired.
∴ We will multiply 768 by 3 to get perfect square.
New number = 768 × 3 = 2304
Now each prime factor has a pair. Therefore, 768 × 3 = 2304 is a perfect square.
Thus the required smallest number is 3.
⇒ √2304 = 2 × 2 × 2 × 2 × 3 = 48

6. For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620

Solution –

(i) 252

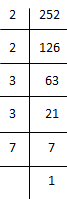
252 = 2 × 2 × 3 × 3 × 7
= (2×2) × (3×3) × 7
Here, 7 cannot be paired.
∴ We will divide 252 by 7 to get perfect square. New number = 252 ÷ 7 = 36
36 = 2 × 2 × 3 × 3
⇒ 36 = (2×2) × (3×3)
⇒ 36 = 2²×3²
⇒ 36 = (2×3)²
⇒ √36 = 2×3 = 6

(ii) 2925

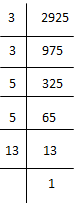
2925 = 3 × 3 × 5 × 5 × 13
= (3×3) × (5×5) × 13
Here, 13 cannot be paired.
∴ We will divide 2925 by 13 to get perfect square. New number = 2925 ÷ 13 = 225
225 = 3 × 3 × 5 × 5
⇒ 225 = (3×3) × (5×5)
⇒ 225 = 3² × 5²
⇒ 225 = (3 × 5)²
⇒ √36 = 3 × 5 = 15

(iii) 396

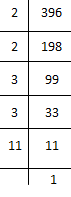
396 = 2 × 2 × 3 × 3 × 11
= (2×2) × (3×3) × 11
Here, 11 cannot be paired.
∴ We will divide 396 by 11 to get perfect square. New number = 396 ÷ 11 = 36
36 = 2×2×3×3
⇒ 36 = (2×2)×(3×3)
⇒ 36 = 2²×3²
⇒ 36 = (2×3)²
⇒ √36 = 2×3 = 6

(iv) 2645

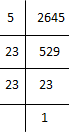
2645 = 5 × 23 × 23
⇒ 2645 = (23×23) × 5
Here, 5 cannot be paired.
∴ We will divide 2645 by 5 to get perfect square.
New number = 2645 ÷ 5 = 529
529 = 23 × 23
⇒ 529 = (23)²
⇒ √529 = 23

(v) 2800

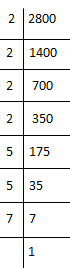
2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
= (2×2) × (2×2) × (5×5) × 7
Here, 7 cannot be paired.
∴ We will divide 2800 by 7 to get perfect square. New number = 2800 ÷ 7 = 400
400 = 2 × 2 × 2 × 2 × 5 × 5
⇒ 400 = (2×2)×(2×2)×(5×5)
⇒ 400 = (2×2×5)²
⇒ √400 = 20

(vi) 1620

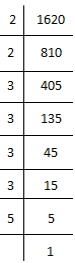
1620 = 2×2×3×3×3×3×5
= (2×2) × (3×3) × (3×3) × 5
Here, 5 cannot be paired.
∴ We will divide 1620 by 5 to get perfect square. New number = 1620 ÷ 5 = 324
324 = 2×2×3×3×3×3
⇒ 324 = (2×2) × (3×3) × (3×3)
⇒ 324 = (2 × 3 × 3)²
⇒ √324 = 18

7. The students of Class VIII of a school donated Rs 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.

Solution – Let the number of students in the school be, x.
Rupees donated by student = x
Total many contributed by all the students= x × x = x²
Given, x² = Rs.2401

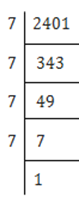
x² = 7×7×7×7
⇒ x² = (7×7)×(7×7)
⇒ x² = 49×49
⇒ x = √(49×49)
⇒ x = 49
∴ The number of students = 49

8. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.

Solution –  Let the number of rows be, x.
number of plants in each row = x.
Total many contributed by all the students = x × x =x²
Given, x² = Rs. 2025

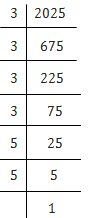
x² = 3×3×3×3×5×5
⇒ x² = (3×3)×(3×3)×(5×5)
⇒ x² = (3×3×5)²
⇒ x = √45 × 45
⇒ x = 45
∴ The number of rows = 45 and the number of plants in each rows = 45.

9. Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.

Solution –

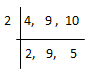
L.C.M of 4, 9 and 10 is (2 × 2 × 9 × 5) = 180.
180 = 2×2×9×5
= (2×2)×(3×3)×5
Here, 5 cannot be paired.
∴ we will multiply 180 by 5 to get perfect square.
Hence, the smallest square number divisible by 4, 9 and 10 = 180×5 = 900

10. Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.

Solution –

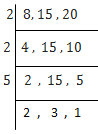
L.C.M of 8, 15 and 20 is (2×2×5×2×3) = 120.
120 = 2×2×3×5×2
= (2×2)×3×5×2
Here, 3, 5 and 2 cannot be paired.
∴ We will multiply 120 by (3×5×2) 30 to get perfect square.
Hence, the smallest square number divisible by 8, 15 and 20 =120×30 = 3600