NCERT Solutions Class 8 Mathematics
Chapter – 10 (Visualising Solid Shapes)
The NCERT Solutions in English Language for Class 8 Mathematics Chapter – 10 Visualising Solid Shapes Exercise 10.3 has been provided here to help the students in solving the questions from this exercise.
Chapter 10: Visualising Solid Shapes
Exercise – 10.3
1. Can a polyhedron have for its faces:
(i) 3 Triangles?
(ii) 4 triangles?
(iii) A square and four triangles?
Solution –
(i) No, such polyhedrons are not possible. Such figures should have minimum 4 faces.
(ii) Yes, a triangular pyramid has 4 triangular faces.
(iii) Yes, as square pyramid has a square face and 4 triangular faces.
2. Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid)
Solution – It is possible, only if the number of faces is greater than or equal to 4.
3. Which are prisms among the following:
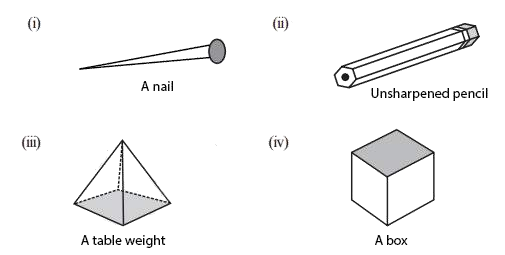
Solution –
(i) A nail: Not a polyhedron as it has a curved surface. This is not a prism.
(ii) Unsharpened Pencil: It is a prism.
(iii) A table Weight: It is not a prism.
(iv) A Box: It is a prism.
4.
(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Solution –
(i) A prism and a cylinder are alike because it can be considered as a circular prism having a curved face. Thus the opposite faces are congruent and parallel.
(ii) A pyramid and a cone are alike because it can be considered as a circular pyramid having a vertex at the top with a lateral curved face.
5. Is a square prism same as a cube? Explain.
Solution – No; not always as it can be a cuboid also.
6. Verify Euler’s formula for these solids.

Solution –
(i) Number of faces, F = 7
Number of edges, E = 15
Number of vertices, V = 10
As per formula, F + V – E = 2
Substitute the values, we have
F + V – E
= 7 + 10 – 15
= 2
Hence, verified.
(ii) Here, F = 9, V = 9 and E = 16
Using formula, F+ V – E = 2
F + V – E
= 9 + 9 – 16
= 2
Hence, Euler’s formula is verified.
7. Using Euler’s formula, find the unknown:
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
Solution – Euler’s formula: F + V – E = 2
Where, F = Faces, V = Vertices and E = Edges
(i) F + 6 – 12 = 2
F = 2 + 6
⇒ F = 8
(ii) 5 + V – 9 = 2
V – 4 = 2
⇒ V = 6
(iii) 20 + 12 – E = 2
32 – E = 2
⇒ E = 30
8. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Solution – From the given data, we have
F = 10
E = 20
V = 15
Every polyhedron satisfies Euler’s formula, which is stated as, F + V – E = 2
For the given polygon,
F + V – E
= 10 + 15 – 20
= 25 – 20
= 5, which is not equal to 2
Therefore, A polyhedron is not possible as Euler’s formula is not satisfied.

Leave a Reply