NCERT Solutions Class 7 Maths Chapter 9 Rational Numbers Ex 9.1

NCERT Solutions Class 7 Mathematics 
Chapter – 9 (Rational Numbers)

The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 9 Rational Numbers Exercise 9.1 has been provided here to help the students in solving the questions from this exercise. 

Chapter : 9 Rational Numbers

Exercise – 9.1 

1. List five rational numbers between:
(i) -1 and 0
(ii) -2 and -1
(iii) \mathbf{\frac{-4}{5}} and \mathbf{\frac{-2}{3}}
(iv) \mathbf{\frac{1}{2}} and \mathbf{\frac{2}{3}}

Solution –

(i) -1 and 0
Converting each of rational numbers as a denominator 5 + 1 = 6,
we have
-1 = \frac{-1\times 6}{6} = \frac{-6}{6} and \frac{0\times 6}{6} = \frac{0}{6}

\frac{-6}{6} < \frac{-5}{6} < \frac{-4}{6} < \frac{-3}{6} < \frac{-2}{6} < \frac{-1}{6} < \frac{0}{6}

or

-1 < \frac{-5}{6} < \frac{-4}{6} < \frac{-3}{6} < \frac{-2}{6} < \frac{-1}{6} < 0

Hence,
the Five Rational numbers between -1 and 0 are  \frac{-5}{6} , \frac{-4}{6} , \frac{-3}{6} , \frac{-2}{6} and  \frac{-1}{6} 

(ii) -2 and -1
Converting each of rational numbers as a denominator 5 + 1 = 6,
We have
-2 = \frac{-2\times 6}{6} = \frac{-12}{6} and \frac{-1\times 6}{6} = \frac{-6}{6} = -1

\frac{-12}{6} < \frac{-11}{6} < \frac{-10}{6} < \frac{-9}{6} < \frac{-8}{6} < \frac{-7}{6} < \frac{-6}{6}

or

-2 < \frac{-11}{6} < \frac{-10}{6} < \frac{-9}{6} < \frac{-8}{6} < \frac{-7}{6} < -1

Hence,
the Five Rational numbers between -2 and -1 are \frac{-11}{6} , \frac{-10}{6} , \frac{-9}{6} , \frac{-8}{6} and \frac{-7}{6} 

(iii) \mathbf{\frac{-4}{5}} and \mathbf{\frac{-2}{3}}
Converting each of the rational numbers as a denominator (L.C.M. of 5 and 3) = 15,
we have
\frac{-4}{5} = \frac{-4\times 3}{5\times 3} = \frac{-12}{15} and \frac{-2\times 5}{3\times 5}= \frac{-10}{15}

Since there is only one integer i.e. -11 between -12 and -10, we have to find equivalent rational numbers.

\frac{-12}{15} = \frac{-12\times3}{15\times 3} = \frac{-36}{45} and \frac{-10\times 3}{15\times 3} = \frac{-30}{45}

\frac{-36}{45} < \frac{-35}{45} < \frac{-34}{45} < \frac{-33}{45} < \frac{-32}{45} < \frac{-31}{45} < \frac{-30}{45}

or

\frac{-4}{5} < \frac{-35}{45} < \frac{-34}{45} < \frac{-33}{45} < \frac{-32}{45} < \frac{-31}{45} < \frac{-2}{3}

Hence,
the Five Rational numbers between \frac{-4}{5}  and \frac{-2}{3} are \frac{-35}{45} , \frac{-34}{45} , \frac{-33}{45} , \frac{-32}{45} and \frac{-31}{45}  

(iv) \mathbf{\frac{1}{2}} and \mathbf{\frac{2}{3}}

Converting each of the rational numbers in their equivalent rational numbers,
we have

\frac{1}{2} = \frac{1\times 3}{2\times 3} = \frac{3}{6} and  \frac{2}{3} =  \frac{2\times 2}{3\times 2} = \frac{4}{6}

Since there is only one integer i.e. 3 between 4, we have to find equivalent rational numbers.

\frac{3}{6} = \frac{3\times 6}{6\times 6} = \frac{18}{36} and \frac{4}{6} = \frac{4\times 6}{6\times 6} = \frac{24}{36}

∴ \frac{18}{36} < \frac{19}{36} < \frac{20}{36} < \frac{21}{36} < \frac{22}{36} < \frac{23}{36} < \frac{24}{36}

or

∴ \frac{1}{2}  < \frac{19}{36} < \frac{5}{9} < \frac{7}{12} < \frac{11}{18} < \frac{23}{36} < \frac{2}{3}

Hence,
the Five Rational numbers between \frac{1}{2}  and  \frac{2}{3}  are \frac{19}{36} , \frac{5}{9} , \frac{7}{12} , \frac{11}{18} and \frac{23}{36}

 

2. Write four more rational numbers in each of the following patterns:

(i) \mathbf{\frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15},\frac{-12}{20}, ....}

(ii) \mathbf{\frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}, ...}

(iii) \mathbf{\frac{-1}{6}, \frac{2}{-12},\frac{3}{-18},\frac{4}{-24}...}

(iv) \mathbf{\frac{-2}{3},\frac{2}{-3},\frac{4}{-6},\frac{6}{-9},...}

Solution –

(i) \mathbf{\frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15},\frac{-12}{20}, ....}

In the above question, we can observe that the numerator and denominator are the multiples of 3 and 5.

= \frac{-3\times 1}{5\times 1}, \frac{-3\times 2}{5\times 2}, \frac{-3\times 3}{5\times 3}, \frac{-3\times 4}{5\times 4},...

Then, next four rational numbers in this pattern are,

= \frac{-3\times 5}{5\times 5}, \frac{-3\times 6}{5\times 6}, \frac{-3\times 7}{5\times 7}, \frac{-3\times 8}{5\times 8}

= \frac{-15}{25}, \frac{-18}{30},\frac{-21}{35}, \frac{-24}{40}

(ii) \mathbf{\frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}, ...}

In the above question, we can observe that the numerator and denominator are the multiples of 1 and 4.

= \frac{-1\times 1}{4\times 1}, \frac{-1\times 2}{4\times 2}, \frac{-1\times 3}{4\times 3}, ...

Then, next four rational numbers in this pattern are,

= \frac{-1\times4}{4\times 4}, \frac{-1\times 5}{4\times 5}, \frac{-1\times 6}{4\times 6}, \frac{-1\times 7}{4\times 7}

= \frac{-4}{16},\frac{-5}{20},\frac{-6}{24},\frac{-7}{28}

(iii) \mathbf{\frac{-1}{6}, \frac{2}{-12},\frac{3}{-18},\frac{4}{-24}...}

In the above question, we can observe that the numerator and denominator are the multiples of 1 and 6.

= \frac{-1\times 1}{6\times 1},\frac{1\times 2}{6\times -2}, \frac{-1\times 3}{6\times -3}, \frac{-1\times 4}{6\times -4}

Then, next four rational numbers in this pattern are,

= \frac{-1\times 5}{6\times 5},\frac{1\times 6}{6\times -6}, \frac{-1\times 7}{6\times -7}, \frac{-1\times 8}{6\times -8}

= \frac{-5}{30},\frac{6}{-36},\frac{7}{-42},\frac{8}{-48}

(iv) \mathbf{\frac{-2}{3},\frac{2}{-3},\frac{4}{-6},\frac{6}{-9},...}

In the above question, we can observe that the numerator and denominator are the multiples of 2 and 3.

= \frac{-2\times 1}{3\times 1},\frac{2\times 1}{-3\times 1}, \frac{2\times 2}{-3\times 2},\frac{2\times 3}{-3\times 3}...

Then, next four rational numbers in this pattern are,

= \frac{2\times 4}{-3\times 4},\frac{2\times 5}{-3\times 5}, \frac{2\times 6}{-3\times 6},\frac{2\times 7}{-3\times 7},

= \frac{8}{-12},\frac{10}{-15},\frac{12}{-18},\frac{14}{-21}

3. Give four rational numbers equivalent to:

(i) \boldsymbol{\frac{-2}{7}}                           (ii) \mathbf{\frac{5}{-3}}                         (iii) \mathbf{\frac{4}{9}}

Solution –

(i) \boldsymbol{\frac{-2}{7}}

The four rational numbers equivalent to \frac{-2}{7} are,

= \frac{-2\times 2}{7\times 2},\frac{-2\times 3}{7\times 3}, \frac{-2\times 4}{7\times 4}, \frac{-2\times 5}{7\times 5}

= \frac{-4}{14},\frac{-6}{21},\frac{-8}{28},\frac{-10}{35}

(ii) \mathbf{\frac{5}{-3}}

The four rational numbers equivalent to \frac{5}{-3} are,

= \frac{5\times 2}{-3\times 2},\frac{5\times 3}{-3\times 3}, \frac{5\times 4}{-3\times 4},\frac{5\times 5}{-3\times 5}

= \frac{10}{-6},\frac{15}{-9},\frac{20}{-12},\frac{25}{-15}

(iii) \mathbf{\frac{4}{9}}

The four rational numbers equivalent to \frac{4}{9} are,

= \frac{4\times 2}{9\times 2},\frac{4\times 3}{9\times 3}, \frac{4\times 4}{9\times 4},\frac{4\times 5}{9\times 5}

= \frac{8}{18},\frac{12}{27},\frac{16}{36},\frac{20}{45}

4. Draw the number line and represent the following rational numbers on it:

(i) \mathbf{\frac{3}{4}}                 (ii) \mathbf{\frac{-5}{8}}

(iii) \mathbf{\frac{-7}{4}}          (iv) \mathbf{\frac{7}{8}}

Solution –

(i) \mathbf{\frac{3}{4}}

We know that \frac{3}{4}  is greater than 0 and less than 1.
∴ it lies between 0 and 1. It can be represented on number line as,
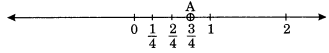
NCERT Class 7 Maths Solution

(ii) \mathbf{\frac{-5}{8}}

We know that \frac{-5}{8} is less than 0 and greater than -1.
∴ it lies between 0 and -1. It can be represented on number line as,
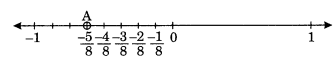
NCERT Class 7 Maths Solution

(iii) \mathbf{\frac{-7}{4}}

Now above question can be written as, \frac{-7}{4} = -1\frac{3}{4} 

We know that \frac{-7}{4} is Less than -1 and greater than -2.
∴ it lies between -1 and -2. It can be represented on number line as,
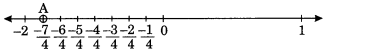
NCERT Class 7 Maths Solution

(iv) \mathbf{\frac{7}{8}}

We know that 7/8 is greater than 0 and less than 1.
∴ it lies between 0 and 1. It can be represented on number line as,
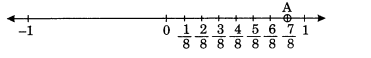
NCERT Class 7 Maths Solution

5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
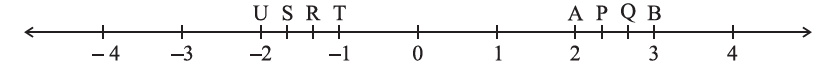
NCERT Class 7 Maths Solution

Solution –
The distance between A and B = 1 unit
And it is divided into 3 equal parts = AP = PQ = QB = \frac{1}{3}
P = 2 + \frac{1}{3} = \frac{(6+1)}{3} = \frac{7}{3}

Q = 2 + \frac{2}{3} = \frac{(6+2)}{3} = \frac{8}{3}

Similarly,
The distance between U and T = 1 unit
And it is divided into 3 equal parts = TR = RS = SU = \frac{1}{3}
R = – 1 – \frac{1}{3} = \frac{(-3-1)}{3} = \frac{-4}{3}

S = – 1 – \frac{2}{3}  = \frac{(-3-2)}{3} = \frac{-5}{3}

6. Which of the following pairs represent the same rational number?

(i) \mathbf{\frac{-7}{21}} and \mathbf{\frac{3}{9}}

(ii) \mathbf{\frac{-16}{20}} and \mathbf{\frac{20}{-25}}

(iii) \mathbf{\frac{-2}{-3}}  and \mathbf{\frac{2}{3}}

(iv) \mathbf{\frac{-3}{5}} and \mathbf{\frac{-12}{20}}

Solution –

(i) \mathbf{\frac{-7}{21}} and \mathbf{\frac{3}{9}}

LCM of 21 and 9 = 189

⇒ \frac{-7\times 9}{21\times 9} and \frac{3\times 21}{9\times 21}

⇒  \frac{-63}{189} and \frac{63}{189}

Since – 63 ≠ 63,

So,   \frac{-7}{21} and \frac{3}{9}  pair is not represents the same rational number.

(ii) \mathbf{\frac{-16}{20}} and \mathbf{\frac{20}{-25}}

LCM of 20 and 25 = 100

⇒ \frac{-16\times 5}{20\times 5} and \frac{20\times 4}{-25\times 4}

⇒  \frac{-80}{100} and \frac{80}{-100} 

⇒-\frac{80}{100} and -\frac{80}{100}

Since – 80 = 80,

So,   \frac{-16}{20} and \frac{20}{-25}  pair is represents the same rational number.

(iii) \mathbf{\frac{-2}{-3}}  and \mathbf{\frac{2}{3}}

Here, we have the same numerator and denominator. So \frac{-2}{-3} = \frac{2}{3} and \frac{2}{3} represents the same rational number.

(iv) \mathbf{\frac{-3}{5}} and \mathbf{\frac{-12}{20}}

LCM of 5 and 20 = 20

⇒ \frac{-3\times 4}{5\times 4} and \frac{-12}{20}

⇒  \frac{-12}{20} and \frac{-12}{20}  

Since – 12 = – 12,

So,   \frac{-3}{5} and \frac{-12}{20} pair is represents the same rational number.

(v) \mathbf{\frac{8}{-5}} and \mathbf{\frac{-24}{15}}

LCM of 5 and 15 = 15

⇒ \frac{8\times 3}{-5\times 3} and \frac{-24}{15}

⇒  \frac{24}{-15} and \frac{-24}{15}

⇒ -\frac{24}{15} and -\frac{24}{15}

Since 24 = 24,

So, \frac{8}{-5} and \frac{-24}{15} pair is represents the same rational number.

(vi) \mathbf{\frac{1}{3}} and \mathbf{\frac{-1}{9}}

LCM of 3 and 9 = 9

⇒ \frac{1\times 3}{3\times 3} and \frac{-1}{9}

⇒  \frac{3}{9} and \frac{-1}{9}

Since 3 ≠ -1,

So, \frac{1}{3} and \frac{-1}{9} pair is not represents the same rational number.

(vii) \mathbf{\frac{-5}{-9}} and \mathbf{\frac{5}{-9}}

⇒ \frac{-5}{-9} = \frac{5}{9} and \frac{5}{-9}

Since 5 ≠ -5,

So, \frac{-5}{-9} and \frac{5}{-9} pair is not represents the same rational number.

7. Rewrite the following rational numbers in the simplest form:

(i) \mathbf{\frac{-8}{6}}                    (ii) \mathbf{\frac{25}{45}}

Solution –

(i) \mathbf{\frac{-8}{6}}

⇒ \frac{-8\div2}{6\div2} = \frac{-4}{3}  [\because HCF of 8 and 6 = 2]

(ii) \mathbf{\frac{25}{45}}

⇒ \frac{25\div5}{45\div5} = \frac{5}{9}  [\because HCF of 25 and 45 = 5]

(iii) \mathbf{\frac{-44}{72}}

⇒ \frac{-44\div4}{72\div4} = \frac{-11}{18}  [\because HCF of 44 and 72 = 4]

(iv) \mathbf{\frac{-8}{10}}

⇒ \frac{-8\div2}{10\div2}  = \frac{-4}{5}  [\because HCF of 8 and 10 = 2]

 

8. Fill in the boxes with the correct symbol out of >, <, and =.

(i) \mathbf{\frac{-5}{7}} [ ] \mathbf{\frac{2}{3}}                       (ii) \mathbf{\frac{-4}{5}} [ ] \mathbf{\frac{-5}{7}}            (iii)  \mathbf{\frac{-7}{8}} [ ] \mathbf{\frac{14}{-16}}

(iv) \mathbf{\frac{-8}{5}} [ ] \mathbf{\frac{-7}{4}}                 (v) \mathbf{\frac{1}{-3}} [ ] \mathbf{\frac{-1}{4}}             (vi) \mathbf{\frac{5}{-11}} [ ] \mathbf{\frac{-5}{11}}

(vii) 0 [ ] \mathbf{\frac{-7}{6}}

Solution –

(i) \mathbf{\frac{-5}{7}} [ ] \mathbf{\frac{2}{3}}
The LCM of the denominators 7 and 3 is 21
∴ \frac{-5}{7} = \frac{-5 \times 3}{7 \times 3} = \frac{-15}{21}

and

\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}

Now, -15 < 14

So, \frac{-15}{21} < \frac{14}{21}

Hence, \frac{-5}{7} [<] \frac{2}{3}

(ii) \mathbf{\frac{-4}{5}} [ ] \mathbf{\frac{-5}{7}}

The LCM of the denominators 5 and 7 is 35

∴ \frac{-4}{5} = \frac{-4\times 7}{5\times 7} = \frac{-28}{35}

and

\frac{-5}{7} = \frac{-5\times 5}{7\times 5} = \frac{-25}{35}

Now, -28 < -25

So, \frac{-28}{35} < \frac{-25}{35}

Hence, \frac{-4}{5} [<] \frac{-5}{7}

(iii)  \mathbf{\frac{-7}{8}} [ ] \mathbf{\frac{14}{-16}}

\frac{14}{-16} can be simplified further,
Then,
\frac{7}{-8}             ——- [∵ Divide both numerator and denominator by 2]

So, \frac{-7}{8} = \frac{7}{-8}

Hence, \frac{-7}{8} [=] \frac{14}{-16}

(iv) \mathbf{\frac{-8}{5}} [ ] \mathbf{\frac{-7}{4}}   

The LCM of the denominators 5 and 4 is 20

∴ \frac{-8}{5} = \frac{-8\times 4}{5\times 4} = \frac{-32}{20}

and

\frac{-7}{4} = \frac{-7\times 5}{4\times 5} = \frac{-35}{20}

Now,  – 32 > – 35

So, \frac{-32}{20} > \frac{-35}{20}

Hence, \frac{-8}{5} [>] \frac{-7}{4}

(v) \mathbf{\frac{1}{-3}} [ ] \mathbf{\frac{-1}{4}}     

The LCM of the denominators 3 and 4 is 12
∴ \frac{1}{-3} = \frac{1\times 4}{-3\times 4} = \frac{4}{-12}

and

\frac{-1}{4} = \frac{-1\times 3}{4\times 3} = \frac{-3}{12}

Now, – 4 < – 3

So, \frac{4}{-12} < \frac{-3}{12}

Hence, \frac{1}{-3} [<] \frac{-1}{4}

(vi) \mathbf{\frac{5}{-11}} [ ] \mathbf{\frac{-5}{11}}

Since, \frac{5}{-11} = \frac{-5}{11}

Hence, \frac{5}{-11} [=] \frac{-5}{11}

(vii) 0 [ ] \mathbf{\frac{-7}{6}}

Since every negative rational number is less than 0.
We have  0 [>] \frac{-7}{6}

9. Which is greater in each of the following:

(i) \mathbf{\frac{2}{3}}, \mathbf{\frac{5}{2}}                    (ii) \mathbf{\frac{-5}{6}}, \mathbf{\frac{-4}{3}}           (iii) \mathbf{\frac{-3}{4}}, \mathbf{\frac{2}{-3}}         

(iv) \mathbf{\frac{-1}{4}}, \mathbf{\frac{1}{4}}            (v) \mathbf{-3\frac{2}{7}}, \mathbf{-3\frac{4}{5}}

Solution –

(i) \mathbf{\frac{2}{3}}, \mathbf{\frac{5}{2}}
The LCM of the denominators 3 and 2 is 6

⇒ \frac{2\times 2}{3\times 2}, \frac{5\times 3}{2\times 3}

⇒ \frac{4}{6}, \frac{15}{6}

⇒ 4 < 15

So, \frac{4}{6} < \frac{15}{6}

∴ \frac{2}{3} < \frac{5}{2}

Hence, \frac{5}{2} is greater.

(ii) \mathbf{\frac{-5}{6}}, \mathbf{\frac{-4}{3}}
The LCM of the denominators 6 and 3 is 6

⇒ \frac{-5}{6}, \frac{-4\times 2}{3\times 2}

⇒ \frac{-5}{6}, \frac{-8}{6}

⇒ -5 > -8

So, \frac{-5}{6} > \frac{-8}{6}

∴ \frac{-5}{6}> \frac{-4}{3}

Hence, \frac{-5}{6} is greater.

(iii) \mathbf{\frac{-3}{4}}, \mathbf{\frac{2}{-3}}
The LCM of the denominators 4 and 3 is 12

⇒ \frac{-3\times 3}{4\times 3}, \frac{2\times 4}{-3\times 4}

⇒ \frac{-9}{12}, \frac{8}{-12}

⇒ -9 < -8

So, \frac{-9}{12} < \frac{8}{-12}

∴ \frac{-3}{4} < \frac{2}{-3}

Hence, \frac{2}{-3} is greater.

(iv) \mathbf{\frac{-1}{4}}, \mathbf{\frac{1}{4}}

∴ Each Positive number is greater than its negative 

So, \frac{-1}{4} < \frac{1}{4}

Hence \frac{1}{4} is greater

(v) \mathbf{-3\frac{2}{7}}, \mathbf{-3\frac{4}{5}}

⇒ -\frac{23}{7}, -\frac{19}{5}

The LCM of the denominators 7 and 5 is 35

⇒ \frac{-23\times 5}{7\times 5}, \frac{-19\times 7}{5\times 7}

⇒ \frac{-115}{35}, \frac{-133}{35}

Now, -115 > -133

So, \frac{-115}{35} > \frac{-133}{35}

∴ -3\frac{2}{7} > -3\frac{4}{5} 

Hence, -3\frac{2}{7} is greater.

10. Write the following rational numbers in ascending order:

(i) \mathbf{\frac{-3}{5}}, \mathbf{\frac{-2}{5}}, \mathbf{\frac{-1}{5}}               (ii) \mathbf{\frac{-1}{3}}, \mathbf{\frac{-2}{9}}, \mathbf{\frac{-4}{3}}                        (iii) \mathbf{\frac{-3}{7}}, \mathbf{\frac{-3}{2}}, \mathbf{\frac{-3}{4}}

Solution –

(i) \mathbf{\frac{-3}{5}}, \mathbf{\frac{-2}{5}}, \mathbf{\frac{-1}{5}}

The given rational numbers are in form of like fraction,
Hence,

\frac{-3}{5} < \frac{-2}{5} <\frac{-1}{5}

(ii) \mathbf{\frac{-1}{3}}, \mathbf{\frac{-2}{9}}, \mathbf{\frac{-4}{3}}

LCM of 3, 9, and 3 is 9

⇒ \frac{-1\times 3}{3\times 3}, \frac{-2}{9}, \frac{-4\times 3}{3\times 3}

⇒ \frac{-3}{9}, \frac{-2}{9} , \frac{-12}{9}

Since \frac{-12}{9} < \frac{-3}{9} < \frac{-2}{9}  

Hence, \frac{-4}{3} < \frac{-1}{3} < \frac{-2}{9}

(iii) \mathbf{\frac{-3}{7}}, \mathbf{\frac{-3}{2}}, \mathbf{\frac{-3}{4}}

LCM of 7, 2, and 4 is 28

⇒ \frac{-3\times 4}{7\times 4}, \frac{-3\times 14}{2\times 14}, \frac{-3\times 7}{4\times 7}

⇒ \frac{-12}{28}, \frac{-42}{28}, \frac{-21}{28}

Since \frac{-42}{28} < \frac{-21}{28} <\frac{-12}{28}

Hence, \frac{-3}{2} < \frac{-3}{4} < \frac{-3}{7}

 

 

You might be interested in

Admin

Leave a Reply

Your email address will not be published.

Latest from Class 7 Maths