NCERT Solutions Class 7 Maths Chapter 8 Comparing Quantities Ex 8.2

NCERT Solutions Class 7 Mathematics 
Chapter – 8 (Comparing Quantities)

The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 8 Comparing Quantities Exercise 8.2 has been provided here to help the students in solving the questions from this exercise. 

Chapter : 8 Comparing Quantities

Exercise – 8.2 

1. Convert the given fractional numbers to percent.
(a) \mathbf{\frac{1}{8}}            (b) \mathbf{\frac{5}{4}}            (c) \mathbf{\frac{3}{40}}             (d) \mathbf{\frac{2}{7}}

Solution –
(a) \mathbf{\frac{1}{8}}
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.

⇒ \frac{1}{8} × 100 %

⇒ \frac{100}{8} % = 12.5% or 12\frac{1}{2}% 

(b) \mathbf{\frac{5}{4}}
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.
⇒ \frac{5}{4} × 100 %
⇒ 5 × 25 %
⇒ 125%

(c) \mathbf{\frac{3}{40}}
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.

⇒ \frac{3}{40} × 100 %

⇒ \frac{3}{2} × 5 %

⇒ \frac{15}{2} % = 7.5% or 7\frac{1}{2}%

(d) \mathbf{\frac{2}{7}}
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.
⇒ \frac{2}{7} × 100 %

⇒ \frac{200}{7} % = 28\frac{4}{7} %

2. Convert the given decimal fraction to percent.
(a) 0.65              (b) 2.1               (c) 0.02                  (d) 12.35

Solution –

(a) 0.65
First we have to remove the decimal point,
= \frac{65}{100}
Now,
Multiply by 100 and put the percent sign %.
We have,

= \frac{65}{100} × 100

= 65%

(b) 2.1
First we have to remove the decimal point,
= \frac{21}{10}
Now,
Multiply by 100 and put the percent sign %.
We have,
= \frac{21}{10} × 100
= 210%

(c) 0.02
First we have to remove the decimal point,
= \frac{2}{100}
Now,
Multiply 100 and put the percent sign %.
We have,
= \frac{2}{100} × 100
= 2%

(d) 12.35
First we have to remove the decimal point,
= \frac{1235}{100}
Now,
Multiply by 100 and put the percent sign %.
We have,
= \frac{1235}{100} × 100

= 1235%

3. Estimate what part of the figures is coloured and hence find the per cent which is coloured.
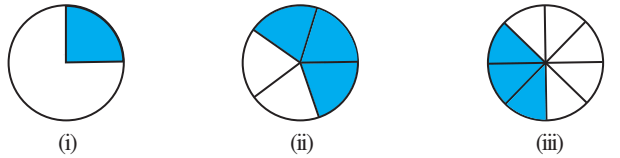
NCERT Class 7 Maths Solution

Solution –
(i) Fraction of coloured part = \frac{1}{4}
∴ Percentage of coloured parts 100
= \frac{1}{4} × 100 = 25%

(ii) Fraction of coloured part = \frac{3}{5}
∴ Percentage of coloured parts
= \frac{3}{5} × 100%
= 3 × 20%
= 60%

(iii) Fraction of coloured part = \frac{3}{8}
∴ Percentage of coloured parts
= \frac{3}{8} × 100%

= \frac{3}{2} \times 25% = \frac{75}{2}%

= 37.5% 

4. Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of ₹ 2500
(d) 75% of 1 kg

Solution –

(a) 15% of 250
We have,
= \frac{15}{100} × 250

= \frac{15}{2} \times 5

= \frac{75}{2}  

= 37.5

(b) 1% of 1 hour
We know that, 1 hour = 60 minutes
Then,
1% of 60 minutes
1 minute = 60 seconds
60 minutes = 60 × 60 = 3600 seconds
1% of 3600 seconds
= \frac{1}{100} × 3600
= 1 × 36
= 36 seconds

(c) 20% of ₹ 2500
= \frac{20}{100} × 2500
= 20 × 25
= ₹ 500

(d) 75% of 1 kg
We know that, 1 kg = 1000 g
Then,
75% of 1000 g
= \frac{75}{100} × 1000
= 75 × 10
= 750 g

5. Find the whole quantity if
(a) 5% of it is 600
(b) 12% of it is? 1080
(c) 40% of it is 500 km
(d) 70% of it is 14 minutes
(e) 8% of it is 40 litres

Solution –

(a) 5% of it is 600
Let us assume the whole quantity be x,
Then,
\frac{5}{100} × (x) = 600

x = 600 × \frac{100}{5}

x = 600 × 20

x = 12000

(b) 12% of it is ₹ 1080.
Let us assume the whole quantity be x,
Then,

\frac{12}{100} × (x) = 1080

x = 1080 × \frac{100}{12}

x = 90 × 100

x = ₹ 9000

(c) 40% of it is 500k km
Let us assume the whole quantity be x,
Then,
\frac{40}{100} × (x) = 500

x = 500 × \frac{100}{40}

x = 500 × \frac{10}{4}

x = 500 × 2.5

x = 1250 km

(d) 70% of it is 14 minutes
Let us assume the whole quantity be x,
Then,
\frac{70}{100} × (x) = 14

x = 14 × \frac{100}{70}

x = 2 × 10
x = 20 minutes

(e) 8% of it is 40 liters
Let us assume the whole quantity be x,
Then,
\frac{8}{100} × (x) = 40

x = 40 × \frac{100}{8}
x = 5 × 100
x = 500 liters

6. Convert given percent to decimal fractions and also fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%

Solution –

(a) 25%
First convert the given percentage into fraction and then put the fraction into decimal form.
= \frac{25}{100}
= ¼
= 0.25

(b) 150%
First convert the given percentage into fraction and then put the fraction into decimal form.
= \frac{150}{100}

= \frac{3}{2} 

= 1.5

(c) 20%
First convert the given percentage into fraction and then put the fraction into decimal form.
= \frac{20}{100}

= \frac{1}{5}

= 0.2

(d) 5%
First convert the given percentage into fraction and then put the fraction into decimal form.
= \frac{5}{100}

= \frac{1}{20}

= 0.05

7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?

Solution –
Percentage of female in a city =30%
Percentage of male in a city = 40%
Total percentage of male and female both = 40% + 30%
= 70%
Now we have to find the percentage of children = 100 – 70
= 30%
So, 30% are children.

8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?

Solution –
Total number of voters in the constituency = 15000
Percentage of people who voted in the election = 60%
Percentage of people who did not voted in the election = 100 – 60
= 40%
Total number of voters who did not voted in the election = 40% of 15000
= \frac{40}{100}  × 15000

= 40 × 150
= 6000 voters
∴ 6000 voters did not vote.

9. Meeta saves ₹ 4000 from her salary. If this is 10% of her salary. What is her salary?

Solution –
Let us assume Meeta’s salary be ₹ x,
Then,
10% of ₹ x = ₹ 4000

\frac{10}{100} × (x) = 4000

x = 4000 × \frac{100}{10}

x = 4000 × 10

x = ₹ 40000
∴ Meeta’s salary is ₹ 40000.

10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?

Solution –
Total matches played by a local team = 20
Percentage of matches won by the local team = 25%
Then,
Number of matches won by the team = 25% of 20

= \frac{25}{100} × 20

= \frac{25}{5}
= 5 matches.

∴ The local team won 5 matches out of 20 matches.

 

You might be interested in

Admin

Leave a Reply

Your email address will not be published.

Latest from Class 7 Maths