NCERT Solutions Class 7 Mathematics
Chapter – 14 (Symmetry)
The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 14 Symmetry Exercise 14.3 has been provided here to help the students in solving the questions from this exercise.
Chapter : 14 Symmetry
Exercise – 14.3
1. Name any two figures that have both line symmetry and rotational symmetry.
Solution – Equilateral triangle and Circle.
2. Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Solution –
(i) a triangle with both line and rotational symmetries of order more than 1.
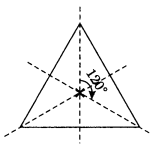
A triangle with both line and rotational symmetries of order more than 1 is an equilateral triangle.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
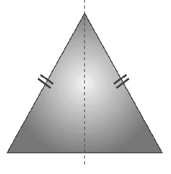
A triangle with only line symmetry and no rotational symmetry of order more than 1 is isosceles triangle.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
A quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry is not possible to draw. Because, a quadrilateral with a line symmetry may have rotational symmetry of order one but not more than one.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
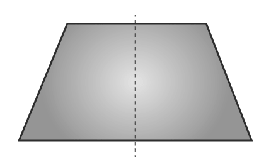
A quadrilateral with line symmetry but not a rotational symmetry of order more than 1 is rhombus.
3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Solution –
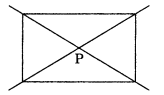
Yes. The above figure has two lines of symmetry and also rotational symmetry of order 2.
4. Fill in the blanks:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral Triangle | |||
| Regular Hexagon | |||
| Circle | |||
| Semi-circle |
Solution:-
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | Intersecting point of diagonals | 4 | 90o |
| Rectangle | Intersecting point of diagonals | 2 | 180o |
| Rhombus | Intersecting point of diagonals | 2 | 180o |
| Equilateral Triangle | Intersecting point of medians | 3 | 120o |
| Regular Hexagon | Intersecting point of diagonals | 6 | 60o |
| Circle | Centre | Infinite | Every angle |
| Semi-circle | Mid-point of diameter | 1 | 360o |
5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Solution – Square, rectangles and rhombus are such quadrilateral which have both line and rotational symmetry.
6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Solution – If a figure is rotated through the angles 120°, 180°, 240°, 300° and 360°, it looks exactly the same.
7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°?
(ii) 17°?
Solution –
(i) 45°?
Yes. We can have a rotational symmetry of order more than 1 whose angle of rotation is 45o.
(ii) 17°?
No. We cannot have a rotational symmetry of order more than 1 whose angle of rotation is 17o.

Leave a Reply