NCERT Solutions Class 7 Mathematics
Chapter – 11 (Perimeter and Area)
The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 11 Perimeter and Area Exercise 11.2 has been provided here to help the students in solving the questions from this exercise.
Chapter : 11 Perimeter and Area
- NCERT Solution Class 7 Maths Exercise – 11.1
- NCERT Solution Class 7 Maths Exercise – 11.3
- NCERT Solution Class 7 Maths Exercise – 11.4
Exercise – 11.2
1. Find the area of each of the following parallelograms:
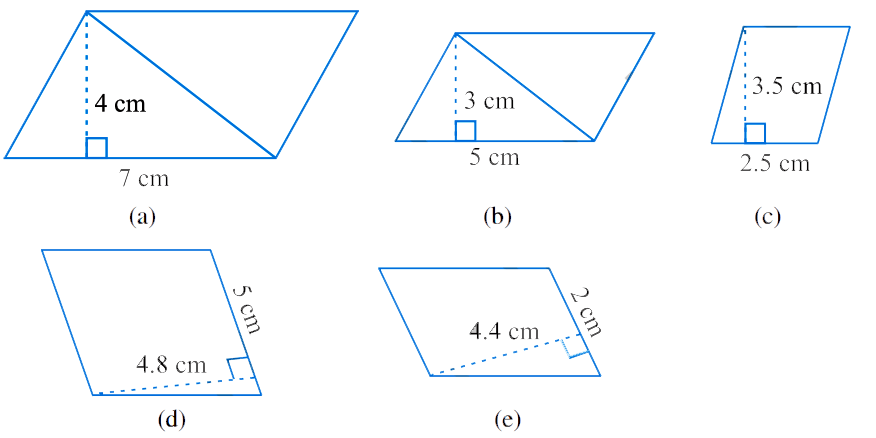
Solution –
From the figure,
(a)
Height of parallelogram = 4 cm
Base of parallelogram = 7 cm
Then,
Area of parallelogram = base × height
= 7 cm × 4 cm
= 28 cm2
(b)
Height of parallelogram = 3 cm
Base of parallelogram = 5 cm
Then,
Area of parallelogram = base × height
= 5 cm × 3 cm
= 15 cm2
(c)
Height of parallelogram = 3.5 cm
Base of parallelogram = 2.5 cm
Then,
Area of parallelogram = base × height
= 2.5 cm × 3.5 cm
= 8.75 cm2
(d)
Height of parallelogram = 4.8 cm
Base of parallelogram = 5 cm
Then,
Area of parallelogram = base × height
= 5 × 4.8
= 24 cm2
(e)
Height of parallelogram = 4.4 cm
Base of parallelogram = 2 cm
Then,
Area of parallelogram = base × height
= 2 cm × 4.4 cm
= 8.8 cm2
2. Find the area of each of the following triangles:
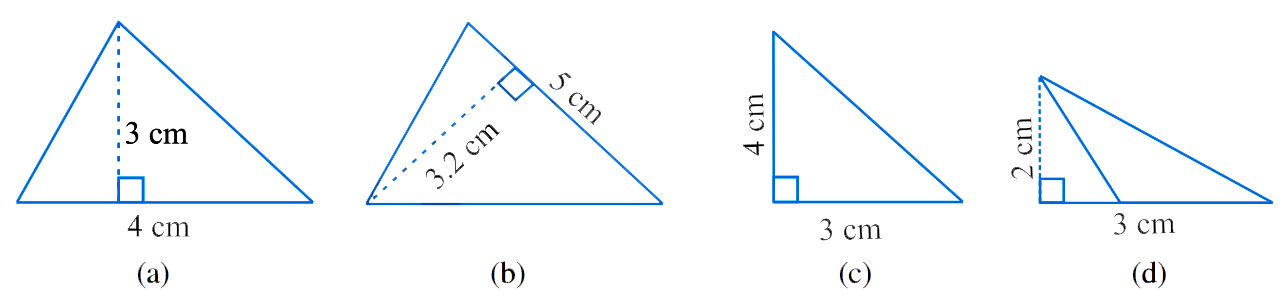
Solution –
From the figure,
(a)
Base of triangle = 4 cm
Height of height = 3 cm
Then,
Area of triangle = ½ × base × height
= ½ × 4 cm × 3 cm
= 1 × 2 cm × 3 cm
= 6 cm2
(b)
Base of triangle = 3.2 cm
Height of height = 5 cm
Then,
Area of triangle = ½ × base × height
= ½ × 3.2 cm × 5 cm
= 1 × 1.6 cm × 5 cm
= 8 cm2
(c)
Base of triangle = 3 cm
Height of height = 4 cm
Then,
Area of triangle = ½ × base × height
= ½ × 3 cm × 4 cm
= 1 × 3 cm × 2 cm
= 6 cm2
(d)
Base of triangle = 3 cm
Height of height = 2 cm
Then, Area of triangle = ½ × base × height
= ½ × 3 cm × 2 cm
= 1 × 3 cm × 1 cm
= 3 cm2
3. Find the missing values:
| S.No. | Base | Height | Area of the Parallelogram |
| a. | 20 cm | ________ | 246 cm2 |
| b. | ________ | 15 cm | 154.5 cm2 |
| c. | ________ | 8.4 cm | 48.72 cm2 |
| d. | 15.6 cm | ________ | 16.38 cm2 |
Solution –
(a)
Base of parallelogram = 20 cm
Height of parallelogram =?
Area of the parallelogram = 246 cm2
Then,
Area of parallelogram = base × height
246 = 20 × height
Height =
Height = 12.3 cm
∴ Height of the parallelogram is 12.3 cm.
(b)
Base of parallelogram =?
Height of parallelogram =15 cm
Area of the parallelogram = 154.5 cm2
Then,
Area of parallelogram = base × height
154.5 = base × 15
Base = cm
Base = 10.3 cm
∴ Base of the parallelogram is 10.3 cm.
(c)
Base of parallelogram =?
Height of parallelogram =8.4 cm
Area of the parallelogram = 48.72 cm2
Then,
Area of parallelogram = base × height
48.72 = base × 8.4
Base = cm
Base = 5.8 cm
∴ Base of the parallelogram is 5.8 cm.
(d)
Base of parallelogram = 15.6 cm
Height of parallelogram =?
Area of the parallelogram = 16.38 cm2
Then,
Area of parallelogram = base × height
16.38 = 15.6 × height
Height =
Height = 1.05 cm
∴ Height of the parallelogram is 1.05 cm.
| S.No. | Base | Height | Area of the Parallelogram |
| a. | 20 cm | 12.3 cm | 246 cm2 |
| b. | 10.3 cm | 15 cm | 154.5 cm2 |
| c. | 5.8 cm | 8.4 cm | 48.72 cm2 |
| d. | 15.6 cm | 1.05 | 16.38 cm2 |
4. Find the missing values:
| Base | Height | Area of Triangle |
| 15 cm | ______ | 87 cm2 |
| ______ | 31.4 mm | 1256 mm2 |
| 22 cm | ______ | 170.5 cm2 |
Solution –
(a)
Height of triangle =?
Base of triangle = 15 cm
Area of the triangle = 16.38 cm2
Then,
Area of triangle = ½ × base × height
87 = ½ × 15 × height
Height = =
Height = 11.6 cm
∴ Height of the triangle is 11.6 cm.
(b)
Height of triangle =31.4 mm
Base of triangle =?
Area of the triangle = 1256 mm2
Then,
Area of triangle = ½ × base × height
1256 = ½ × base × 31.4
Base = =
Base = 80 mm = 8 cm
∴ Base of the triangle is 80 mm or 8 cm.
(c)
Height of triangle =?
Base of triangle = 22 cm
Area of the triangle = 170.5 cm2
Then,
Area of triangle = ½ × base × height
170.5 = ½ × 22 × height
170.5 = 1 × 11 × height
Height =
Height = 15.5 cm
∴ Height of the triangle is 15.5 cm.
5. PQRS is a parallelogram (Fig 11.23). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
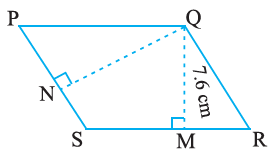
(a) The area of the parallelogram PQRS
(b) QN, if PS = 8 cm
Solution –
Given that,
SR = 12 cm,
QM = 7.6 cm
(a) Area of the parallelogram = base × height
= SR × QM
= 12 cm × 7.6 cm
= 91.2 cm2
(b) Area of the parallelogram = base × height
91.2 = PS × QN
91.2 = 8 × QN
QN =
QN = 11.4 cm
6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (Fig 11.24). If the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BM and DL.
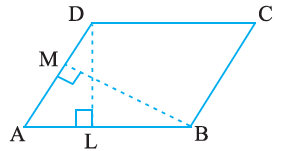
Solution –
Given that,
Area of the parallelogram = 1470 cm2
AB = 35 cm
AD = 49 cm
Then,
Area of the parallelogram = base × height
1470 = AB × BM
1470 = 35 × DL
DL =
DL = 42 cm
And,
Area of the parallelogram = base × height
1470 = AD × BM
1470 = 49 × BM
BM =
BM = 30 cm
7. ΔABC is right angled at A (Fig 11.25). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.
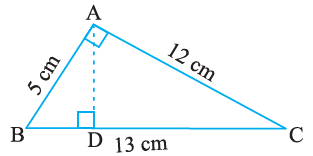
Solution –
Given that,
AB = 5 cm, BC = 13 cm, AC = 12 cm
Then,
Area of the ΔABC = ½ × base × height
= ½ × AB × AC
= ½ × 5 cm × 12 cm
= 1 × 5 cm × 6 cm
= 30 cm2
Now,
Area of ΔABC = ½ × base × height
30 = ½ × AD × BC
30 = ½ × AD × 13
= AD
AD = = 4.6 cm
8. ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (Fig 11.26). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
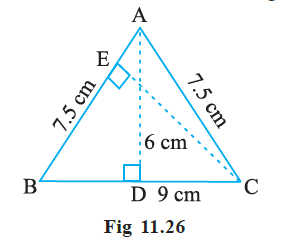Solution –
Given that,
AB = AC = 7.5 cm, BC = 9 cm, AD = 6cm
Then,
Area of ΔABC = ½ × base × height
= ½ × BC × AD
= ½ × 9 cm × 6 cm
= 1 × 9 cm × 3 cm
= 27 cm2
Now,
Area of ΔABC = ½ × base × height
27 = ½ × AB × CE
27 = ½ × 7.5 × CE
= CE
CE =
CE = 7.2 cm
