NCERT Solutions Class 7 Maths
Chapter – 1 (Integers)
The NCERT Solutions in English Language for Class 7 Mathematics Chapter – 1 Integers Exercise 1.1 has been provided here to help the students in solving the questions from this exercise.
Chapter 1: Integers
- NCERT Solution Class 7 Maths Exercise – 1.2
- NCERT Solution Class 7 Maths Exercise – 1.3
- NCERT Solution Class 7 Maths Exercise – 1.4
Exercise – 1.1
1. Following number line shows the temperature in degree celsius (co) at different places on a particular day.
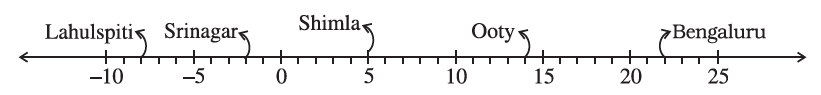
(a) Observe this number line and write the temperature of the places marked on it.
Solution –
| Cities | Temperature |
| Lahulspriti | -8°C |
| Srinagar | -2°C |
| Shimla | 5°C |
| Ooty | 14°C |
| Bengaluru | 22°C |
(b) What is the temperature difference between the hottest and the coldest places among the above?
Solution –
The temperature at the hottest place i.e., Bengaluru = 22oC
The temperature at the coldest place i.e., Lahulspiti = -8oC
Temperature difference between hottest and coldest place is = 22oC – (-8oC)
= 22oC + 8oC
= 30oC
Hence, the temperature difference between the hottest and the coldest place is 30oC.
(c) What is the temperature difference between Lahulspriti and Srinagar?
Solution –
The temperature at the Lahulspiti is -8oC
The temperature at the Srinagar is -2oC
∴ The temperature difference between Lahulspiti and Srinagar is = -2oC – (8oC)
= – 2OC + 8oC
= 6oC
(d) Can we say temperature of Srinagar and Shimla taken together is less than the temperature at Shimla? Is it also less than the temperature at Srinagar?
Solution –
Temperature of Srinagar = -2°C
Temperature of Shimla = 5°C
∴ Temperature of the above cities taken together
= -2°C + 5°C = 3°C
Temperature of Shimla = 5°C
Hence, the temperature of Srinagar and Shimla taken together is less than that of Shimla by 2°C.
i.e., (5°C – 3°C) = 2°C
2. In a quiz, positive marks are given for correct answers and negative marks are given for incorrect answers. If Jack’s scores in five successive rounds were 25, – 5, – 10, 15 and 10, what was his total at the end?
Solution –
Given Jack’s scores are 25, -5, -10, 15, 10
The total score of Jack at the end will be = 25 + (-5) + (-10) + 15 + 10
= 25 – 5 – 10 + 15 + 10
= 50 – 15
= 35
∴ Jack’s total score at the end is 35.
3. At Srinagar temperature was – 5°C on Monday and then it dropped by 2°C on Tuesday. What was the temperature of Srinagar on Tuesday? On Wednesday, it rose by 4°C. What was the temperature on this day?
Solution –
Initial temperature of Srinagar on Monday = -5°C
Temperature on Tuesday at Srinagar is dropped by 2oC = Temperature on Monday – 2oC
Temperature on Tuesday = -5°C – 2°C = -7°C
Temperature on Wednesday at Srinagar is rose by 4oC = Temperature on Tuesday + 4oC
∴ Temperature on Wednesday = -7°C + 4°C = -3°C
Thus, the temperature on Tuesday and Wednesday was -7oC and -3oC respectively.
4. A plane is flying at the height of 5000 m above the sea level. At a particular point, it is exactly above a submarine floating 1200 m below the sea level. What is the vertical distance between them?
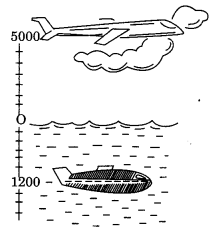
Solution –
Height of the flying plane = 5000 m
Depth of the submarine = -1200 m
∴ Distance between them
= + 5000 m – (-1200 m)
= 5000 m + 1200 m = 6200 m
Hence, the vertical distance = 6200 m
5. Mohan deposits ₹2,000 in his bank account and withdraws ₹1,642 from it, the next day. If withdrawal of amount from the account is represented by a negative integer, then how will you represent the amount deposited? Find the balance in Mohan’s account after the withdrawal.
Solution –
The deposited amount will be represented by a positive integer i.e., ₹2000.
Amount withdrawn = ₹1,642
∴ Balance in the account
= ₹2,000 – ₹1,642 = ₹358
Hence, the balance in Mohan’s account after the withdrawal is ₹358
6. Rita goes 20 km towards east from a point A to the point B. From B, she moves 30 km towards west along the same road. If the distance towards east is represented by a positive integer then, how will you represent the distance travelled towards west? By which integer will you represent her final position from A?

Solution:-
Rita travels a distance in east direction = 20 km
Rita travels a distance in west direction = – 30 km
∴ Distance travelled from A = 20 + (- 30)
= 20 – 30
= – 10 km
Hence, the required position of Rita will be presented by a negative number, i.e., -10 km.
7. In a magic square each row, column and diagonal have the same sum. Check which of the following is a magic square.
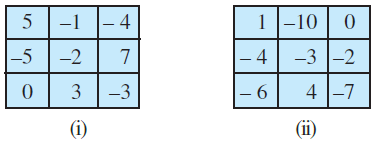
Solution –
First we consider the square (i)
By adding the numbers in each rows we get,
= 5 + (- 1) + (- 4) = 5 – 1 – 4 = 5 – 5 = 0
= -5 + (-2) + 7 = – 5 – 2 + 7 = -7 + 7 = 0
= 0 + 3 + (-3) = 3 – 3 = 0
By adding the numbers in each columns we get,
= 5 + (- 5) + 0 = 5 – 5 = 0
= (-1) + (-2) + 3 = -1 – 2 + 3 = -3 + 3 = 0
= -4 + 7 + (-3) = -4 + 7 – 3 = -7 + 7 = 0
By adding the numbers in diagonals we get,
= 5 + (-2) + (-3) = 5 – 2 – 3 = 5 – 5 = 0
= -4 + (-2) + 0 = – 4 – 2 = -6
Because sum of one diagonal is not equal to zero, So, Square (i) is not a magic square.
Now, we consider the square (ii)
By adding the numbers in each rows we get,
= 1 + (-10) + 0 = 1 – 10 + 0 = -9
= (-4) + (-3) + (-2) = -4 – 3 – 2 = -9
= (-6) + 4 + (-7) = -6 + 4 – 7 = -13 + 4 = -9
By adding the numbers in each columns we get,
= 1 + (-4) + (-6) = 1 – 4 – 6 = 1 – 10 = -9
= (-10) + (-3) + 4 = -10 – 3 + 4 = -13 + 4
= 0 + (-2) + (-7) = 0 – 2 – 7 = -9
By adding the numbers in diagonals we get,
= 1 + (-3) + (-7) = 1 – 3 – 7 = 1 – 10 = -9
= 0 + (-3) + (-6) = 0 – 3 – 6 = -9
This square (ii) is a magic square, because sum of each row, each column and diagonal is equal to -9.
8. Verify a – (– b) = a + b for the following values of a and b.
(i) a = 21, b = 18
(ii) a = 118, b = 125
(iii) a = 75, b = 84
(iv) a= 28, 6 = 11
Solution –
(i) a = 21, b = 18
a – (-b) = a + b
LHS = 21 – (-18) = 21 + 18 = 39
RHS = 21 + 18 = 39
LHS = RHS Hence, verified.
(ii) a = 118, b = 125
a – (-b) = a + b
LHS = 118 – (-125) = 118 + 125 = 243
RHS = 118 + 125 = 243
LHS = RHS Hence, verified.
(iii) a = 75, b = 84
a – (-b) = a + b
LHS = 75 – (-84) = 75 + 84 = 159
RHS = 75 + 84 = 159
LHS = RHS Hence, verified.
(iv) a= 28, 6 = 11
a – (-b) = a + b
LHS = 28 – (-11) = 28 + 11 = 39
RHS = 28 + 11 = 28 + 11 = 39
LHS = RHS Hence, verified.
9. Use the sign of >, < or = in the box to make the statements true.
(a) (-8) + (-4) [ ] (-8) – (-4)
(b) (-3) + 7 – (19) [ ] 15 – 8 + (-9)
(c) 23 – 41 + 11 [ ] 23 – 41 – 11
(d) 39 + (-24) – (15) [ ] 36 + (-52) – (-36)
(e) -231 + 79 + 51 [ ] -399 + 159 + 81
Solution –
(a) (-8) + (-4) [ ] (-8) – (-4)
LHS = (-8) + (-4) = -8 – 4 = – 12
RHS = (-8) – (-4) = -8 + 4 = -4
Here – 12 < -4
Hence, (-8) + (-4) [<] (-8) – (-4)
(b) (-3) + 7 – (19) [ ] 15 – 8 + (-9)
LHS = (-3) + 7 – (19) = -3 + 7 – 19
= -3 – 19 + 7
= -22 + 1 = -15
RHS = 15 – 8 + (-9)
= 15-8-9
= 15 – 17 = -2
Here -15 < -2
Hence, (-3) + 7 – (19) [<] 15 – 8 + (-9)
(c) 23 – 41 + 11 [ ] 23 – 41 – 11
LHS = 23 – 41 + 11
= 23 + 11 – 41
= 34 – 41 = -7
RHS = 23 – 41 – 11
= 23 – 52 = -29
Here, -7 > -29
Hence, 23 – 41 + 11 [>] 23 – 41 – 11
(d) 39 + (-24) – (15) [ ] 36 + (-52) – (-36)
LHS = 39 + (-24) – (15)
= 39 – 24 – 15
= 39 – 39 = 0
RHS = 36 + (-52) – (-36) = 36 – 52 + 36
= 36 + 36 – 52
= 72 – 52 = 20
Here 0 < 20
Hence, 39 + (-24) – (15) [<] 36 + (-52) – (-36)
(e) -231 + 79 + 51 [ ] -399 + 159 + 81
LHS = -231 + 79 + 51 = -231 + 130 = -101
RHS = -399 + 159 + 81 = -399 + 240 = -159
Here, -101 > -159
Hence, -231 + 79 + 51 [>] -399 + 159 + 81
10. A water tank has steps inside it. A monkey is sitting on the topmost step (i.e., the first step). The water level is at the ninth step.

(i) He jumps 3 steps down and then jumps back 2 steps up. In how many jumps will he reach the water level?
Solution –
Initially monkey is sitting on the top most step i.e., first step
In 1st jump monkey will be at step = 1 + 3 = 4 steps
In 2nd jump monkey will be at step = 4 + (-2) = 4 – 2 = 2 steps
In 3rd jump monkey will be at step = 2 + 3 = 5 steps
In 4th jump monkey will be at step = 5 + (-2) = 5 – 2 = 3 steps
In 5th jump monkey will be at step = 3 + 3 = 6 steps
In 6th jump monkey will be at step = 6 + (-2) = 6 – 2 = 4 steps
In 7th jump monkey will be at step = 4 + 3 = 7 steps
In 8th jump monkey will be at step = 7 + (-2) = 7 – 2 = 5 steps
In 9th jump monkey will be at step = 5 + 3 = 8 steps
In 10th jump monkey will be at step = 8 + (-2) = 8 – 2 = 6 steps
In 11th jump monkey will be at step = 6 + 3 = 9 steps (Water level)
Hence the required number of jumps = 11.
(ii) After drinking water, he wants to go back. For this, he jumps 4 steps up and then jumps back 2 steps down in every move. In how many jumps will he reach back the top step?
Solution –
Initially monkey is sitting on the ninth step i.e., at the water level
In 1st jump monkey will be at step = 9 + (-4) = 9 – 4 = 5 steps
In 2nd jump monkey will be at step = 5 + 2 = 7 steps
In 3rd jump monkey will be at step = 7 + (-4) = 7 – 4 = 3 steps
In 4th jump monkey will be at step = 3 + 2 = 5 steps
In 5th jump monkey will be at step = 5 + (-4) = 5 – 4 = 1 step
∴ Monkey took 5 jumps to reach back the top step i.e., first step.
(iii) If the number of steps moved down is represented by negative integers and the number of steps moved up by positive integers, represent his moves in part (i) and (ii) by completing the following; (a) – 3 + 2 – … = – 8 (b) 4 – 2 + … = 8. In (a) the sum (– 8) represents going down by eight steps. So, what will the sum 8 in (b) represent?
Solution –
From the question, it is given that
If the number of steps moved down is represented by negative integers and the number of steps moved up by positive integers.
Monkey moves in part (i)
= – 3 + 2 – ……….. = – 8
Then LHS = – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3
= – 18 + 10
= – 8
RHS = -8
∴ Moves in part (i) represents monkey is going down 8 steps. Because negative integer.
Now,
Monkey moves in part (ii)
= 4 – 2 + ……….. = 8
Then LHS = 4 – 2 + 4 – 2 + 4
= 12 – 4
= 8
RHS = 8
∴ Moves in part (ii) represents monkey is going up 8 steps. Because positive integer.

Leave a Reply