NCERT Solutions Class 11 Maths
The NCERT Solutions in English Language for Class 11 Mathematics Chapter – 3 Trigonometric Functions Exercise 3.1 has been provided here to help the students in solving the questions from this exercise.
Chapter 3 (Trigonometric Functions)
| Exercise – 3.1 |
1. Find the radian measures corresponding to the following degree measures:
(i) 25°
(ii) –47°30′
(iii) 240°
(iv) 520°
Solution –
(i) 25°
As we know that 180° = π radian
So,
1° = π/180° radian
Then, 25° = (π/180°) × 25°
= 5π/36 radians
Hence, 25° equals to 5π/36 radians.
(ii) –47°30′
As we know that 180° = π radian
So,
1° = π/180°
And 60′ = 1°
30′ = (1/2)°
So, -47°30′ = -47 (1/2)°
-47(1/2)° = (π/180) × (-95/2)
= (-19π/72) radian.
Hence, -47°30′ is equals to -19π/72 radian.
(iii) 240°
As we know that 180° = π radian
1° = π/180° radian
So
240° = (π/180°) × 240°
= 4π/3 radians
Hence, 240° equals to 4π/3 radians.
(iv) 520°
As we know that 180° = π radian
1° = π/180° radian
So,
520° = (π/180°) × 520°
= 26π/9 radians
Hence, 520° equals to 26π/9 radians.
2. Find the degree measures corresponding to the following radian measures (Use π = 22/7)
(i) 11/16
(ii) -4
(iii) 5π/3
(iv) 7π/6
Solution –
(i) 11/16
= (11/16) (180°/π) {as 180° = π radian, then 1 radian = 180°/π}
= (11/16) × (180° × 7/22)
= (11 × 180° × 7/16 × 22)
= 315/8°
= 39 (3/8)°
= 39(3/8)°
= 39° + (3/8)°
Again 1° = 60′
So
(3/8)° = 60′ × (3/8)
= 22 (1/2)’
= 22 (1/2)’
= 22′ + 1/2′
Again 1′ = 60″
= (1/2)’ = 30″
Hence, 11/16 radian results to 39° 22′ 30″.
(ii) -4
= -4 × (180°/π) {as 180° = π radian, then 1 radian = 180°/π}.
= -4 ×180° × 7/22
= -229° (1/11)
= -229 (1/11)°= -229° + (1/11)°
Again(1/11)° = (1/11) × 60′. {as 1° = 60′}
= 5(5/11)’
Also, 5 (5/11)’ = 5′ + (5/11)’
(5/11)’ = (5/11) × 60″ {as 1′ = 60″}
= 27″
So, -229(1/11) = -229° 5’27”
Hence, -4 radian results to -229° 5′ 27″.
(iii) 5π/3
= (5 π/3) × (180/π) {as 180° = π radian, then 1 radian =180°/π}.
= (5 × 180/3)°
= 300°
Hence, 5π/3 results to 300°.
(iv) 7π/6
= (7π/6) × (180°/π) {as 180° = π radian, then 1 radian =180°/π}.
= (7 × 180/6)°
= 210°
Hence, 7π/6 radian results to 210°.
3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Solution – It is given that
Total revolutions made by the wheel in one minute is 360.
1 second = 360/6 = 60
We know that
When a wheel revolves once it covers 2π radian of distance.
In one minute, it will turn an angle of 360 × 2π radian = 720 π radian
In one second, it will turn an angle of 720 π radian/60 = 12 π radian {as 1 minute = 60 seconds}
Hence, in one second, the wheel turns an angle of 12π radian.
4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (Use π = 22/7).
Solution – The radius of circle (r) = 100 cm.
Length of the arc (l) = 22 cm.
Let us consider the angle subtended by the arc is θ.
Also, we know that θ = l/r
The angle subtended (θ) = 22/100 radian
For finding the degree measure we have to multiply 180°/π with radian measure
So,
θ = (22/100) × (180/π)
θ = (22/100) × (180 × 7/22)
θ = (22 × 180 × 7/22 × 100)
θ = 126/10 degree
θ = 12 (3/5) degree
We know that 1° = 60′
(3/5)° = 60′ × (3/5) = 36′
So
12 (3/5)° = 12° 36′
Hence, the degree measure of the angle subtended at the Centre of a circle is 12° 36′
5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Solution –
Diameter of circle (d) = 40 cm
Radius (r) = d/2 = 40/2 = 20 cm
Let us consider AB as the chord of circle having length 20 cm, and Centre at O.
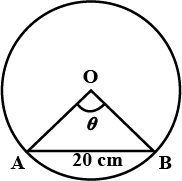
It forms a triangle OAB,
Having Radius = OA = OB = 20 cm
Also, chord AB = 20 cm
Hence, In ΔOAB OA = OB = AB. (equilateral triangle.)
So angle subtend = (π/3) radian
We know that θ = l/r (where θ = angle subtended by the arc, l = length of arc, r = radius)
Putting values of r and θ we get
π/3 = l/20
So.
l = 20 π/3
Hence, length of the arc is 20π/3 cm.
6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Solution – Given that
Angle subtend by 1st arc (θ1) = 60
Angle subtend by 2nd arc (θ2) = 75
We know that θ = l/r
For 1st arc θ1 = l1/r1
For 2nd arc θ2 = l2/r2
θ1/θ2 = (l1/r1)/(l2/r2)
θ1/θ2 = (l/r1)/(l/r2) {here l1 = l2 = l}
θ1/θ2 = r2/r1
60/75 = r2/r1
r2/r1 = 4/5
r1/r2 = 5/4
Hence, ratio of their radius is 5:4.
7. Find the angle in radian though which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm
Solution – In a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = 1/r
We know that r = 75 cm
(i) Given that
Length of an arc (l) = 10 cm
Radius which represents length of pendulum(r) = 75
As We know that θ = l/r
So θ = 10/75 = 2/15 rad
Hence, θ = 2/15 rad
(ii) Given that
Length of an arc (l) = 15 cm
Radius which represents length of pendulum (r) = 75
As We know that θ = l/r
So θ = 15/75 = 1/5 rad
Hence, θ = 1/5 rad
(iii) Given that
Length of an arc (l) = 21 cm
Radius which represents length of pendulum(r) = 75
As We know that θ = l/r
So θ = 21/75 = 7/25 rad
Hence, θ = 7/25 radian

Leave a Reply