NCERT Solutions Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

NCERT Solutions Class 10 Maths
Chapter – 5 (Arithmetic Progressions)

The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 5 Arithmetic Progressions Exercise 5.3 has been provided here to help the students in solving the questions from this exercise.

Chapter : 5 Arithmetic Progressions

Exercise – 5.3

1. Find the sum of the following APs.
(i) 2, 7, 12 ,…., to 10 terms.
(ii) − 37, − 33, − 29 ,…, to 12 terms
(iii) 0.6, 1.7, 2.8 ,…….., to 100 terms
(iv) 1/15, 1/12, 1/10, …… , to 11 terms

Solution –

(i) 2, 7, 12 ,…., to 10 terms.
First term, a = 2
Common difference, d = a₂ − a₁ = 7 − 2 = 5
n = 10
Sum of n^th term in AP series is,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₀ = 10/2 [2(2) + (10 -1)×5]
= 5[4 + (9)×(5)]
= 5 × 49
= 245

(ii) − 37, − 33, − 29 ,…, to 12 terms
First term, a = −37
Common difference, d = a₂− a₁d = (−33) − (−37)
d = − 33 + 37
d = 4
n = 12
Sum of n^th term in AP series is,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₂ = 12/2 [2(-37) + (12 – 1)×4]
= 6[-74 + 11×4]
= 6[-74 + 44]
= 6(-30)
= -180

(iii) 0.6, 1.7, 2.8 ,…….., to 100 terms
First term, a = 0.6
Common difference, d = a₂ − a₁ = 1.7 − 0.6 = 1.1
n = 100
Sum of n^th term in AP series is,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₂ = 50/2 [1.2 + (99)×1.1]
= 50[1.2 + 108.9]
= 50[110.1]
= 5505

(iv) 1/15, 1/12, 1/10, …… , to 11 terms
First term, a = 1/5
Common difference, d = a₂– a₁ = (1/12) – (1/5) = 1/60
n = 11
Sum of n^th term in AP series is,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$

S₁₁ = $\frac{11}{2}\left [ 2\times \frac{1}{15} + \frac{(11-1)1}{60}\right ]$

= 11/2(2/15 + 10/60)
= 11/2 (9/30)
= 33/20

2. Find the sums given below:
(i) $7 + 10\frac{1}{2} + 14+ ...... + 84$
(ii) 34 + 32 + 30 + ……….. + 10
(iii) − 5 + (− 8) + (− 11) + ………… + (− 230)

Solution –
(i) $7 + 10\frac{1}{2} + 14+ ...... + 84$
First term, a = 7
Common difference, d = a₂ – a₁ = 10 $\frac{1}{2}$ – 7
d = 21/2 – 7
d = 7/2
n^th term, a_n= 84
a_n= a(n – 1)d
84 = 7 + (n – 1) × 7/2
77 = (n – 1) × 7/2
22 = n − 1
n = 23
We know that the sum of n term is;
S_n = $\frac{n}{2}\left [ a + l) \right ]$
l = 84
S_n = 23/2 (7 + 84)
S_n = (23 × 91/2)
S_n = 2093/2
S_n = 1046 $\frac{1}{2}$

(ii) 34 + 32 + 30 + ……….. + 10
First term, a = 34
Common difference, d = a₂− a₁ = 32 − 34 = −2
a_n= l = 10
a_n= a + (n − 1)d
10 = 34 + (n − 1)(−2)
−24 = (n −1)(−2)
12 = n −1
n = 13
We know that the sum of n terms is;
S_n = $\frac{n}{2}\left [ a + l) \right ]$
S_n = 13/2 (34 + 10)
S_n = (13 × 44/2)
S_n = 13 × 22
= 286

(iii) − 5 + (− 8) + (− 11) + ………… + (− 230)
a = −5
a_n= l = −230
Common difference, d = a₂− a₁ = (−8)−(−5)
d = − 8 + 5 = −3
Let us assume −230 be the nth term of this A.P.
a_n= a + (n − 1)d
−230 = − 5 + (n − 1)(−3)
−225 = (n − 1)(−3)
(n − 1) = 75
n = 76
And the sum of n term,
S_n = $\frac{n}{2}\left [ a + l) \right ]$
S_n = 76/2 [(-5) + (-230)]
S_n = 38(-235)
S_n = -8930

3. In an AP
(i) Given a = 5, d = 3, a_n = 50, find n and S_n.
(ii) Given a = 7, a₁₃ = 35, find d and S₁₃.
(iii) Given a₁₂ = 37, d = 3, find a and S₁₂.
(iv) Given a₃ = 15, S₁₀ = 125, find d and a₁₀.
(v) Given d = 5, S₉ = 75, find a and a₉.
(vi) Given a = 2, d = 8, S_n = 90, find n and a_n.
(vii) Given a = 8, a_n = 62, S_n = 210, find n and d.
(viii) Given a_n = 4, d = 2, S_n = − 14, find n and a.
(ix) Given a = 3, n = 8, S = 192, find d.
(x) Given l = 28, S = 144 and there are total 9 terms. Find a.

Solution –

(i) Given a = 5, d = 3, a_n = 50, find n and S_n.
a = 5
d = 3
a_n = 50
a_n = a + (n − 1)d,
⇒ 50 = 5 + (n – 1)×3
⇒ 3(n – 1) = 45
⇒ n – 1 = 15
⇒ n = 16
Now, sum of n terms,
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
S_n = 16/2 (5 + 50)
S_n = 8 × 55
S_n = 440

(ii) Given a = 7, a₁₃ = 35, find d and S₁₃.
a = 7
a₁₃ = 35
a_n = a + (n − 1)d,
⇒ 35 = 7 + (13 – 1)d
⇒ 12d = 28
⇒ d = 28/12 = 2.33
Now, sum of n terms,
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
S₁₃ = 13/2 (7 + 35)
S₁₃ = 6.5 × 42
S₁₃ = 273

(iii) Given a₁₂ = 37, d = 3, find a and S₁₂.
a₁₂ = 37
d = 3
a_n = a + (n − 1)d,
⇒ a₁₂ = a + (12 − 1)3
⇒ 37 = a + 33
⇒ a = 4
Now, sum of n^th term,
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
S_n = 12/2 (4 + 37)
S_n = 6 × 42
S_n = 246

(iv) Given a₃ = 15, S₁₀ = 125, find d and a₁₀.
a₃ = 15
S₁₀ = 125
a_n = a + (n − 1)d,
a₃ = a + (3−1)d
15 = a + 2d ————- (i)
Sum of the n^th term,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₀ = 10/2 [2a + (10 – 1)d]
125 = 5(2a + 9d)
25 = 2a + 9d —————- (ii)
On multiplying equation (i) by (ii), we will get;
30 = 2a + 4d —————- (iii)
By subtracting equation (iii) from (ii), we get,
−5 = 5d
d = −1
From equation (i),
15 = a + 2(−1)
15 = a−2
a = 17 = First term
a₁₀ = a + (10 − 1)d
a₁₀ = 17 + (9)(−1)
a₁₀ = 17 − 9 = 8

(v) Given d = 5, S₉ = 75, find a and a₉.
d = 5
S₉ = 75
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₉ = 9/2 [2a +(9 – 1)5]
25 = 3(a + 20)
25 = 3a + 60
3a = 25 − 60
a = -35/3
As we know, the n^th term can be written as;
a_n = a + (n−1)d
a₉ = a + (9 − 1)(5)
= -35/3 + 8(5)
= -35/3 + 40
= (-35 + 120)/3
= 85/3

(vi) Given a = 2, d = 8, S_n = 90, find n and a_n.
a = 2
d = 8
S_n = 90
As, sum of n terms in an AP is,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
90 = n/2 [2a + (n – 1)d]
⇒ 180 = n(4 + 8n -8)
⇒ 180 = n(8n – 4)
⇒ 180 = 8n²– 4n
⇒ 8n²– 4n –180 = 0
⇒ 2n²– n – 45 = 0
⇒ 2n²– 10n + 9n – 45 = 0
⇒ 2n(n – 5) + 9(n – 5) = 0
⇒ (n – 5)(2n + 9) = 0
So, n = 5 (as n only is a positive integer)
∴ a₅= 8 + 5 × 4
a₅= 34

(vii) Given a = 8, a_n = 62, S_n = 210, find n and d.
a = 8
a_n = 62
S_n = 210
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
210 = n/2 (8 + 62)
⇒ 35n = 210
⇒ n = 210/35
⇒ n = 6
Now, 62 = 8 + 5d
⇒ 5d = 62 – 8
⇒ 5d = 54
⇒ d = 54/5
⇒ d = 10.8

(viii) Given a_n = 4, d = 2, S_n = − 14, find n and a.
a_n = 4
d = 2
S_n = −14.
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
a_n = a + (n −1)d,
⇒ 4 = a + (n − 1)2
⇒ 4 = a + 2n − 2
⇒ a + 2n = 6
⇒ a = 6 − 2n —————- (i)
As we know, the sum of n terms is;
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
-14 = n/2 (a + 4)
−28 = n (a + 4)
−28 = n (6 −2n + 4) {From equation (i)}
−28 = n (− 2n + 10)
−28 = − 2n²+ 10n
2n² −10n − 28 = 0
n² − 5n −14 = 0
n² − 7n + 2n −14 = 0
n (n − 7) + 2(n − 7) = 0
(n − 7)(n + 2) = 0
Either n − 7 = 0 or n + 2 = 0
n = 7 or n = −2
However, n can neither be negative nor fractional.
Therefore, n = 7
From equation (i), we get
a = 6 − 2n
a = 6 − 2(7)
a = 6−14
a = −8

(ix) Given a = 3, n = 8, S = 192, find d.
a = 3
n = 8
S_n = 192
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
192 = 8/2 [2 × 3 + (8 -1)d]
192 = 4[6 + 7d]
48 = 6 + 7d
42 = 7d
d = 6

(x) Given l = 28, S = 144 and there are total 9 terms. Find a.
l = a_n= 28
S_n = 144
n = 9
S_n = $\frac{n}{2}\left [ a + a_n) \right ]$
144 = 9/2 (a + 28)
16 × 2 = a + 28
32 = a + 28
a = 4

4. How many terms of the AP. 9, 17, 25 … must be taken to give a sum of 636?

Solution – Let there be n terms of the AP. 9, 17, 25 …
a = 9
d = a₂− a₁ = 17 − 9 = 8
S_n =
636 = n/2 [2×9 + (n – 1)×8]
636 = n/2 [18 + (n – 1)×8]
636 = n [9 + 4n −4]
636 = n (4n +5)
4n² + 5n −636 = 0
4n² + 53n −48n −636 = 0
n (4n + 53) − 12 (4n + 53) = 0
(4n + 53)(n − 12) = 0
4n + 53 = 0 or n − 12 = 0
n = (-53/4) or n = 12
n cannot be negative or fraction, therefore, n = 12 only.

5. The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.

Solution – Given :
a = 5
l = 45
S_n = 400
S_n = $\frac{n}{2}\left [ a + l) \right ]$
400 = n/2 (5 + 45)
400 = n/2 (50)
n = 16
a_n = l = a + (n −1)d
45 = 5 +(16 −1)d
40 = 15d
d = 40/15 = 8/3

6. The first and the last term of an AP are 17 and 350, respectively. If the common difference is 9, how many terms are there and what is their sum?

Solution – Given :
a = 17
d = 9
l = 350
a_n = l = a + (n −1)d
350 = 17 + (n −1)9
333 = (n − 1)9
(n−1) = 37
n = 38
S_n = $\frac{n}{2}\left [ a + l) \right ]$
S₃₈ = 38/2 (17 + 350)
S₃₈ = 19×367
S₃₈ = 6973
Thus, this A.P. contains 38 terms and the sum of the terms of this A.P. is 6973.

7. Find the sum of first 22 terms of an AP in which d = 7 and 22^nd term is 149.

Solution – Given:
d = 7
a₂₂ = 149
S₂₂ = ?
a_n = a + (n − 1)d
a₂₂ = a + (22 − 1)d
149 = a + 21×7
149 = a + 147
a = 2
S_n = $\frac{n}{2}\left [ a + l) \right ]$
S₂₂ = 22/2 (2 + 149)
S₂₂ = 11×151
S₂₂ = 1661

8. Find the sum of the first 51 terms of an AP whose second and third terms are 14 and 18, respectively.

Solution – Given :
a₂ = 14
a₃ = 18
d = a₃− a₂ = 18 − 14 = 4
a₂ = a + d
14 = a + 4
a = 10
Sum of n terms
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₅₁ = 51/2 [2×10 + (51 – 1) 4]
S₅₁ = 51/2 [20 + (50)×4]
S₅₁ = 51 × 220/2
S₅₁ = 51 × 110
S₅₁ = 5610

9. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.

Solution – Given :
S₇ = 49
S₁₇ = 289
We know, sum of n terms;
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₇= 7/2 [2a + (n – 1)d]
49 = 7/2 [2a + (7 – 1)d]
49 = 7/2 [2a + 6d]
7 = (a + 3d)
a + 3d = 7 ——————(i)

S₁₇ = 17/2 [2a + (17 – 1)d]
289 = 17/2 (2a + 16d)
17 = (a + 8d)
a + 8d = 17 ——————(ii)
Subtracting equation (i) from equation (ii),
(a + 8d) – (a + 3d) = 17 – 7
5d = 10
d = 2
From equation (i), we can write it as;
a + 3(2) = 7
a + 6 = 7
a = 1
Hence,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S_n = n/2[2(1) + (n – 1)×2]
= n/2(2 + 2n – 2)
= n/2(2n)
= n²

10. Show that a₁, a₂… , a_n , … form an AP where a_n is defined as below
(i) a_n = 3+4n
(ii) a_n = 9 − 5n
Also, find the sum of the first 15 terms in each case.

Solution –

(i) a_n = 3+4n
a₁ = 3 + 4(1) = 7
a₂ = 3 + 4(2) = 3 + 8 = 11
a₃ = 3 + 4(3) = 3 + 12 = 15
a₄ = 3 + 4(4) = 3 + 16 = 19
We can see here, the common difference between the terms are;
a₂ − a₁ = 11 − 7 = 4
a₃ − a₂ = 15 − 11 = 4
a₄ − a₃ = 19 − 15 = 4
Hence, a_k_{+ 1} − a_k is the same value every time. Therefore, this is an AP with common difference as 4 and first term as 7.
Now, we know, the sum of nth term is;
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₅= 15/2 [2(7) + (15 – 1)×4]
S₁₅= 15/2[(14) + 56]
S₁₅= 15/2 (70)
S₁₅= 15 × 35
S₁₅= 525

(ii) a_n = 9 − 5n
a₁ = 9 − 5×1 = 9−5 = 4
a₂ = 9−5×2 = 9−10 = −1
a₃ = 9−5×3 = 9−15 = −6
a₄ = 9−5×4 = 9−20 = −11
We can see here, the common difference between the terms are;
a₂ − a₁ = −1−4 = −5
a₃ − a₂ = −6−(−1) = −5
a₄ − a₃ = −11−(−6) = −5
Hence, a_k_{+ 1} − a_k is same every time. Therefore, this is an A.P. with common difference as −5 and first term as 4.
Now, we know, the sum of nth term is;
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₅= 15/2[2(4) + (15 – 1)(-5)]
S₁₅= 15/2[8 + 14(-5)]
S₁₅= 15/2(8 – 70)
S₁₅= 15/2(-62)
S₁₅= 15(-31)
S₁₅= -465

11. If the sum of the first n terms of an AP is 4n − n², what is the first term (that is S₁)? What is the sum of first two terms? What is the second term? Similarly find the 3^rd, the 10^th and the n^th terms.

Solution – Given :
S_n = 4n − n²a = S₁ = 4(1) − (1)² = 4 − 1 = 3
S₂= 4(2) − (2)² = 8 − 4 = 4
a₂ = S₂ − S₁ = 4 − 3 = 1
d = a₂− a = 1 − 3 = −2
N^th term, a_n = a + (n − 1)d
= 3 + (n − 1)(−2)
= 3 − 2n + 2
= 5 − 2n
Therefore, a₃ = 5 − 2(3) = 5 – 6 = −1
a₁₀ = 5 − 2(10) = 5 − 20 = −15
Hence, the sum of first two terms is 4. The second term is 1.
The 3^rd, the 10^th, and the n^th terms are −1, −15, and 5 − 2n respectively.

12. Find the sum of the first 40 positive integers divisible by 6.

Solution – The first positive integers that are divisible by 6 are 6, 12, 18, 24 ….
a = 6
d = 6
S₄₀ = ?
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
Therefore, putting n = 40, we get,
S₄₀= 40/2 [2(6) + (40 – 1)6]
S₄₀= 20[12 + (39)(6)]
S₄₀= 20(12 + 234)
S₄₀= 20 × 246
S₄₀= 4920

13. Find the sum of first 15 multiples of 8.

Solution – The first few multiples of 8 are 8, 16, 24, 32…
a = 8
d = 8
S₁₅ = ?
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₅ = 15/2 [2(8) + (15 – 1)8]
S₁₅ = 15/2[16 + (14)(8)]
S₁₅ = 15/2[16 + 112]
S₁₅ = 15 (128)/2
S₁₅ = 15 × 64
S₁₅ = 960

14. Find the sum of the odd numbers between 0 and 50.

Solution – The odd numbers between 0 and 50 are 1, 3, 5, 7, 9 … 49.
a = 1
d = 2
l = 49
l = a + (n − 1) d
49 = 1 + (n − 1)2
48 = 2(n − 1)
n − 1 = 24
n = 25
By the formula of sum of nth term, we know,
S_n = $\frac{n}{2}\left [ a + l) \right ]$
S₂₅ = 25/2 (1 + 49)
S₂₅ = 25 (50)/2
S₂₅ = (25)(25)
S₂₅ = 625

15. A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. 200 for the first day, Rs. 250 for the second day, Rs. 300 for the third day, etc., the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much money does the contractor have to pay as penalty, if he has delayed the work by 30 days.

Solution – Given:
a = 200
d = 50
The penalty that has to be paid if the contractor has delayed the work by 30 days = S₃₀S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₃₀= 30/2[2(200) + (30 – 1)50]
S₃₀= 15[400+1450]
S₃₀= 15(1850)
S₃₀= 27750
Therefore, the contractor has to pay Rs 27750 as penalty.

16. A sum of Rs 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.

Solution – Let us assume the cost of 1st prize be Rs. P.
Cost of 2^nd prize = Rs. P − 20
cost of 3^rd prize = Rs. P − 40
These prizes form an A.P., with common difference, d = −20
First term, a = P
S₇ = 700
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
700 = 7/2 [2a + (7 – 1)d]

100 = a + 3(-20)
a − 60 = 100
a = 160
Therefore, the value of each of the prizes was Rs 160, Rs 140, Rs 120, Rs 100, Rs 80, Rs 60, and Rs 40.

17. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees that each section of each class will plant, will be the same as the class, in which they are studying. E.g., a section of class I will plant 1 tree, a section of class II will plant 2 trees and so on till class XII. There are three sections of each class. How many trees will be planted by the students?

Solution – The number of trees planted by the students form an AP, 1, 2, 3, 4, 5………………..12
a = 1
d = 2 − 1 = 1
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₂ = 12/2 [2(1) + (12 – 1)(1)]

S₁₂ = 6(2 + 11)
S₁₂ = 6(13)
S₁₂ = 78
Therefore, the number of trees planted by 1 section of the classes = 78
The number of trees planted by 3 sections of the classes = 3 × 78 = 234
Therefore, 234 trees will be planted by the students.

18. A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A of radii 0.5, 1.0 cm, 1.5 cm, 2.0 cm, ……… as shown in the figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take π = 22/7)

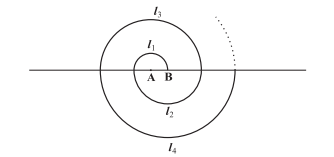
Solution – We know
Perimeter of a semi-circle = πr
P₁ = π(0.5) = π/2 cm
P₂ = π(1) = π cm
P₃ = = π(1.5) = 3π/2 cm
Where, P_1, P₂, P₃ are the lengths of the semi-circles.
Hence we got a series here, as,
π/2, π, 3π/2, 2π, ….
P₁ = π/2 cm
P₂ = π cm
d = P₂– P₁ = π – π/2 = π/2
P₁= a = π/2 cm
By the sum of n term formula, we know,

S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
Therefor, the sum of the length of 13 consecutive circles is;

S₁₃ = 13/2 [2(π/2) + (13 – 1)π/2]

S₁₃ = 13/2 [π + 6π]
S₁₃ = 13/2 (7π)
S₁₃ = 13/2 × 7 × 22/7
S₁₃ = 143 cm

19. 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?

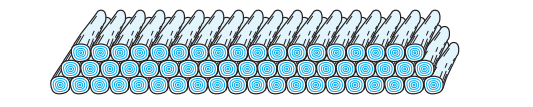
Solution – The numbers of logs in rows are in the form of an A.P. 20, 19, 18…
a = 20
d = a₂− a₁ = 19 − 20 = −1
Let a total of 200 logs be placed in n rows.
Thus, S_n = 200
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₂ = 12/2 [2(20) + (n -1)(-1)]
400 = n (40 − n + 1)
400 = n (41 – n)
400 = 41n − n²n²− 41n + 400 = 0
n²− 16n − 25n + 400 = 0
n(n −16) − 25(n −16) = 0
(n −16)(n −25) = 0
(n −16) = 0 or n − 25 = 0
n = 16 or n = 25
By the nth term formula,
a_n = a + (n − 1)d
a₁₆ = 20 + (16 − 1)(−1)
a₁₆ = 20 − 15
a₁₆ = 5
Similarly, the 25^th term could be written as;
a₂₅ = 20 + (25 − 1)(−1)
a₂₅ = 20 − 24
= −4
It can be seen, the number of logs in the 16^th row is 5 as the numbers cannot be negative.
Therefore, 200 logs can be placed in 16 rows and the number of logs in the 16^th row is 5.

20. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line.

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
[Hint: to pick up the first potato and the second potato, the total distance (in metres) run by a competitor is 2 × 5 + 2 × (5 + 3)]

Solution – The distance of the potatoes from the bucket are 5, 8, 11, 14…, which is in the form of AP.
Now, we know that the distance run by the competitor for collecting these potatoes are two times of the distance at which the potatoes have been kept.
Therefore, distances to be run w.r.t distances of potatoes is equivalent to,
10, 16, 22, 28, 34, ……….
a = 10
d = 16 − 10 = 6
Sum of n^th term, we get,
S_n = $\frac{n}{2}\left [ 2a+(n-1)d \right ]$
S₁₀ = 12/2 [2(20) + (n – 1)(-1)]
S₁₀ = 5[20 + 54]
S₁₀ = 5(74)
S₁₀ = 370
Therefore, the competitor will run a total distance of 370 m.

Go Back To Chapters

NCERT Solutions Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3