NCERT Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

NCERT Solutions Class 10 Maths
Chapter – 3 (Pair of Linear Equations in Two Variables)

The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 3 Pair of Linear Equations in Two Variables Exercise 3.6 has been provided here to help the students in solving the questions from this exercise.

Chapter : 3 Pair of Linear Equations in Two Variables

Exercise – 3.6

1. Solve the following pairs of equations by reducing them to a pair of linear equations:

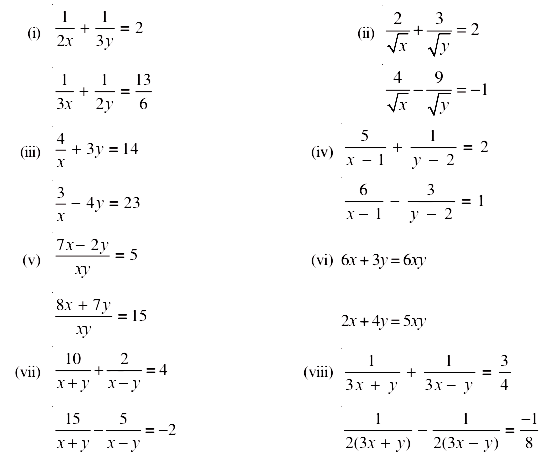
Solution –

(i) $\mathbf{\frac{1}{2x} + \frac{1}{3y}}$ = 2

$\mathbf{\frac{1}{3x}+\frac{1}{2y} = \frac{13}{6}}$
Let us assume 1/x = m and 1/y = n, then the equation will change as follows.
m/2 + n/3 = 2
$\frac{3m + 2n}{6} = 2$
3m + 2n – 12 = 0 ……………. (i)
m/3 + n/2 = 13/6
$\frac{2m + 3n}{6}$ = $\frac{13}{6}$
2m + 3n – 13 = 0 ……………. (ii)
Now, using the cross-multiplication method, we get,
$\frac{m}{(-26 -(-36))} = \frac{n}{(-24-(-39))} = \frac{1}{9-4}$

m/10 = n/15 = 1/5
m/10 = 1/5 and n/15 = 1/5
So, m = 2 and n = 3
1/x = 2 and 1/y = 3
x = 1/2 and y = 1/3

(ii) $\mathbf{\frac{2}{\sqrt{x}} + \frac{3}{\sqrt{y}}} = 2$

$\mathbf{\frac{4}{\sqrt{x}} + \frac{9}{\sqrt{y}}} = -1$

Solution –
Substituting 1/√x = m and 1/√y = n in the given equations, we get
2m + 3n = 2 …………….. (i)
4m – 9n = -1 ……………… (ii)
Multiplying equation (i) by 3, we get
6m + 9n = 6 ….…….….. (iii)
Adding equations (ii) and (iii), we get
10m = 5
m = 1/2 ……….… (iv)
Now, by putting the value of ‘m’ in equation (i), we get
2× ½ + 3n = 2
3n = 1
n = 1/3
m =1/√x
½ = 1/√x
x = 4
n = 1/√y
1/3 = 1/√y
y = 9
Hence, x = 4 and y = 9

(iii) $\mathbf{\frac{4}{x} + 3y = 14}$

$\mathbf{\frac{3}{x} - 4y = 23}$

Solution –
Substituting 1/x = m in the given equation, we get,
4m + 3y = 14
4m + 3y – 14 = 0 ……………… (i)
3m – 4y = 23
3m – 4y – 23 = 0 ………………… (ii)
By cross-multiplication, we get,
m/(-69 – 56) = y/(-42 -(-92)) = 1/(-16-9)
-m/125 = y/50 = -1/ 25
-m/125 = -1/25 and y/50 = -1/25
m = 5 and b = -2
m = 1/x = 5
So ,
x = 1/5
y = -2

(iv) $\mathbf{\frac{5}{(x-1)}+\frac{1}{(y-2)}= 2}$

$\mathbf{\frac{6}{(x-1)}-\frac{3}{(y-2)}= 1}$

Solution –
Substituting 1/(x – 1) = m and 1/(y – 2) = n in the given equations, we get
5m + n = 2 ……………… (i)
6m – 3n = 1 ………………. (ii)
Multiplying equation (i) by 3, we get
15m + 3n = 6 ………………. (iii)
Adding (ii) and (iii), we get
21m = 7
m = 1/3
Putting this value in equation (i), we get
5 × 1/3 + n = 2
n = 2 – 5/3 = 1/3
m = 1/ (x – 1)
1/3 = 1/(x – 1)
x = 4
n = 1/(y – 2)
1/3 = 1/(y – 2)
y = 5
Hence, x = 4 and y = 5

(v) $\mathbf{\frac{7x - 2y}{xy} = 5}$

$\mathbf{\frac{8x + 7y}{xy} = 15}$

Solution –
$\frac{7x - 2y}{xy} = 5$

7/y – 2/x = 5 ………….. (i)

$\frac{8x + 7y}{xy} = 15$

8/y + 7/x = 15 …………… (ii)
Substituting 1/x =m in the given equation, we get
– 2m + 7n = 5
-2 + 7n – 5 = 0 …….. (iii)
7m + 8n = 15
7m + 8n – 15 = 0 …….. (iv)
By cross-multiplication method, we get
m/(-105 – (-40)) = n/(-35 – 30) = 1/(-16 – 49)
m/(-65) = n/(-65) = 1/(-65)
m/-65 = 1/-65
m = 1
n/(-65) = 1/(-65)
n = 1
m = 1 and n = 1
m = 1/x = 1
n = 1/x = 1
Therefore, x = 1 and y = 1

(vi) 6x + 3y = 6xy
2x + 4y = 5xy
Solution –
6x + 3y = 6xy
6/y + 3/x = 6
Let 1/x = m and 1/y = n
6n +3m = 6
3m + 6n – 6 = 0 …………. (i)
2x + 4y = 5xy
2/y + 4/x = 5
2n + 4m = 5
4m + 2n – 5 = 0 ………….. (ii)
3m + 6n – 6 = 0
4m + 2n – 5 = 0
By cross-multiplication method, we get
m/(-30 –(-12)) = n/(-24-(-15)) = 1/(6-24)
m/-18 = n/-9 = 1/-18
m/-18 = 1/-18
m = 1
n/-9 = 1/-18
n = 1/2
m = 1 and n = 1/2
m = 1/x = 1 and n = 1/y = 1/2
x = 1 and y = 2
Hence, x = 1 and y = 2

(vii) $\mathbf{\frac{10}{(x + y)} + \frac{2}{(x-y)} = 4}$

$\mathbf{\frac{15}{(x + y)} + \frac{5}{(x-y)} = -2}$

Solution –
Substituting 1/(x + y) = m and 1/(x – y) = n in the given equations, we get
10m + 2n = 4
10m + 2n – 4 = 0 ………………. (i)
15m – 5n = -2
15m – 5n + 2 = 0 …………….. (ii)
Using the cross-multiplication method, we get
m/(4 – 20) = n/(-60 – (20)) = 1/(-50 -30)
m/-16 = n/-80 = 1/-80
m/-16 = 1/-80 and n/-80 = 1/-80
m = 1/5 and n = 1
m = 1/(x + y) = 1/5
x + y = 5 ………………… (iii)
n = 1/(x – y) = 1
x – y = 1 ……………… (iv)
Adding equations (iii) and (iv), we get
2x = 6
x = 3 ……. (v)
Putting the value of x = 3 in equation (3), we get
y = 2
Hence, x = 3 and y = 2

(viii) $\mathbf{\frac{1}{(3x+y)} + \frac{1}{3x - y} = \frac{3}{4}}$

$\mathbf{\frac{1}{2(3x+y)} + \frac{1}{2(3x - y)} = -\frac{1}{8}}$

Solution –
Substituting 1/(3x + y) = m and 1/(3x – y) = n in the given equations, we get
m + n = 3/4 ……………….…… (i)
m/2 – n/2 = -1/8
m – n = -1/4 ………………..… (ii)
Adding (i) and (ii), we get
2m = 3/4 – 1/4
2m = 1/2
Putting in (ii), we get
1/4 – n = -1/4
n = 1/4 + 1/4 = 1/2
m = 1/(3x + y) = 1/4
3x + y = 4 …………………… (iii)
n = 1/(3x – y) = 1/2
3x – y = 2 …………………… (iv)
Adding equations (iii) and (iv), we get
6x = 6
x = 1 ………………. (5)
Putting in (iii), we get
3(1) + y = 4
y = 1
Hence, x = 1 and y = 1

2. Formulate the following problems as a pair of equations and find their solutions.
(i) Ritu can row downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.

Solutions – Let us consider,
Speed of Ritu in still water = x km/hr
Speed of Stream = y km/hr
Now, the speed of Ritu during
Downstream = x + y km/h
Upstream = x – y km/h
As per the question given,
2(x + y) = 20
x + y = 10 ………………. (i)
2 (x – y) = 4
x – y = 2 …………… (2)
Adding both the eq. (i) and (ii), we get
2x = 12
x = 6
Putting the value of x in eq. (i), we get
y = 4
Therefore,
Speed of Ritu rowing in still water = 6 km/hr
Speed of Stream = 4 km/hr

(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work and also that taken by 1 man alone.

Solutions – Let us consider,
Number of days taken by women to finish the work = x
Number of days taken by men to finish the work = y
Work done by women in one day = 1/x
Work done by women in one day = 1/y
As per the question given,
4(2/x + 5/y) = 1
(2/x + 5/y) = 1/4
(3/x + 6/y) = 1
(3/x + 6/y) = 1/3
Now, put 1/x=m and 1/y=n, we get,
2m + 5n = 1/4
8m + 20n = 1 ……… (i)
3m + 6n = 1/3
9m + 18n = 1 ……. (ii)
Now, by cross multiplication method, we get here,
m/(20 – 18) = n/(9 – 8) = 1/ (180 – 144)
m/2 = n/1 = 1/36
m/2 = 1/36
m = 1/18
m = 1/x = 1/18
x = 18
n = 1/y = 1/36
y = 36
Therefore,
Number of days taken by women to finish the work = 18
Number of days taken by men to finish the work = 36

(iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.

Solutions – Let us consider,
Speed of the train = x km/h
Speed of the bus = y km/h
According to the given question,
60/x + 240/y = 4 ………… (i)
100/x + 200/y = 25/6 ………. (ii)
Put 1/x = m and 1/y = n in the above two equations.
60m + 240n = 4 ………. (iii)
100m + 200n = 25/6
600m + 1200n = 25 ………… (iv)
Multiply eq. (iii) by 10 to get
600m + 2400n = 40 ..………… (v)
Now, subtract eq. (iv) from 5 to get
1200n = 15
n = 15/1200 = 1/80
Substitute the value of n in eq. (iii) to get
60m + 3 = 4
m = 1/60
m = 1/x = 1/60
x = 60
y = 1/n
y = 80
Therefore,
Speed of the train = 60 km/h
Speed of the bus = 80 km/h

Go Back To Chapters

NCERT Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6