NCERT Solutions Class 10 Maths
Chapter – 11 (Constructions)
The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 11 Constructions Exercise 11.2 has been provided here to help the students in solving the questions from this exercise.
Chapter : 11 Constructions
Exercise – 11.2
In each of the following, give also the justification of the construction:
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution – Steps of construction:
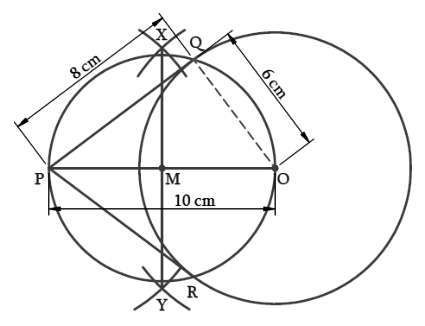
Step I – Take a point O as the centre and 6 cm radius. Draw a circle.
Step II – Take a point P in such a manner that OP = 10cm
Step III – With O and P as centres and radius more than half of OP draw arcs above and below OP to intersect at X and Y.
Step IV – Draw line segment XY to intersect OP at M.
Step V – With M as the centre and OM as radius draw a circle to intersect the given circle at Q and R.
Step VI – Join PQ and PR. PQ and PR are the tangents, where PQ and PR = 8cm.
Proof
Since PQ ⊥ OQ (Angle in a semicircle)
∠PQO = 90º
In right ΔPQO,
OP = 10 cm, OQ = 6cm (radius)
PQ² = OP² – OQ²
= (10)² – (6)²
= 100 – 36
= 64
PQ = √64
= 8 cm
Similarly, we can prove that PR = 8 cm.
2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution – Steps of construction:
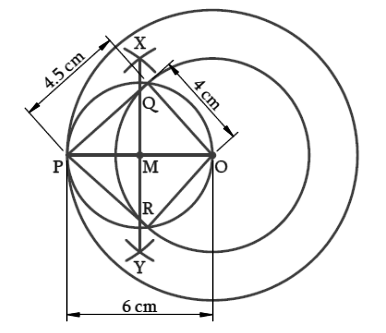
Step I – Take ‘O’ as centre and radius 4 cm and 6 cm respectively to draw two circles.
Step II – Take a point ‘P’ on the bigger circle and join OP.
Step III – With ‘O’ and ‘P’ as centre and radius more than half of OP draw arcs above and below OP to intersect at X and Y.
Step IV – Join XY to intersect OP at M.
Step V – With M as centre and OM as radius draw a circle to cut the smaller circle at Q and R.
Step VI – Join PQ and PR. PQ and PR are the required tangents, where PQ = PR = 4.5 cm (approx.)
Proof
∠PQO = 90º (Angle in a semi-circle)
∴ PQ ⊥ OQ
OQ is the radius of the smaller circle and PQ is the tangent at Q.
In the right ΔPQO,
OP = 6 cm (radius of the bigger circle)
OQ = 4 cm (radius of the smaller circle)
PQ² = (OP)² – (OQ)²
= (6)² – (4)²
= 36 – 16
= 20
PQ = √20
= 4.5 (approx)
Similarly, we can prove PR = 4.5 (approx.)
3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution – Steps of construction:
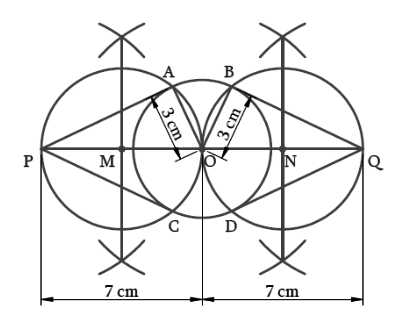
Step I – Draw a circle with O as centre and radius as 3 cm.
Step II – Draw a diameter of it and extend both the sides and mark the points as P, Q such that OP = OQ = 7 cm.
Step III – Draw the perpendicular bisectors of OP and OQ to intersect PQ at M and N respectively.
Step IV – With M as centre and OM as radius draw a circle to cut the given circle at A and C. With N as the centre and ON as radius draw a circle to cut the given circle at B and D.
Step V – Join PA, PC, QB, QD.
PA, PC and QB, QD are the required tangents from P and Q respectively.
Proof
∠PAO = ∠QBO = 90° (Angle in a semi-circle)
∴ PA ⊥ AO, QB ⊥ BO
In right angle triangle PAO,
OP = OQ = 7cm (By construction)
OA = OB = 3cm (radius of the given circle)
PA² = (OP)² – (OA)²
= (7)² – (3)²
= 49 – 9
= 40
PA = √40
= 6.3 (approx.)
Also, in right triangle QBO,
QB² = (OQ)² – (OB)²
= (7)² – (3)²
= 49 – 9
= 40
QB = √40
= 6.3 (approx)
4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution – Steps of construction:
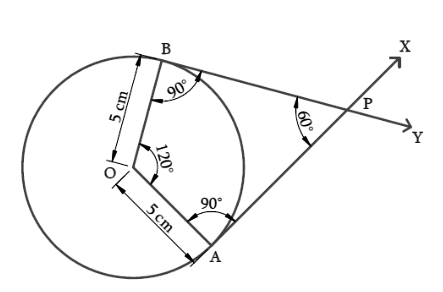
Step I – With O as the centre and 5cm as radius draw a circle.
Step II – Take a point A on the circumference of the circle and join OA.
Step III – Draw AX perpendicular to OA.
Step IV – Construct ∠AOB = 120° where B lies on the circumference.
Step V – Draw BY perpendicular to OB.
Step VI – Both AX and BY intersect at P.
Step VII – PA and PB are the required tangents inclined at 60°.
Proof
∠OAP = ∠OBP = 90° (By construction)
∠AOB = 120° (By construction)
In quadrilateral OAPB,
∠APB = 360° – [∠OAP + ∠OBP + ∠AOB]
= 360° – [90° + 90° + 120°]
= 360° – 300°
= 60°
Hence PA and PB are the required tangents inclined at 60°.
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution – Steps of construction:
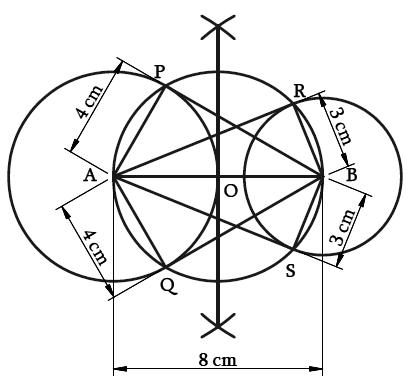
Step I – Draw AB = 8 cm. With A and B as centres, radii as 4 cm and 3 cm respectively draw two circles.
Step II – Draw the perpendicular bisector of AB, intersecting AB at O.
Step III – With O as the centre and OA as radius draw a circle that intersects the two circles at P, Q, R and S.
Step IV – Join BP, BQ, AR and AS.
Step V – BP, BQ are the tangents from B to the circle with centre A.
Step VI – AR, AS are the tangents from A to the circle with centre B.
Proof
∠APB = ∠AQB = 90° (Angle in a semi-circle)
∴ AP ⊥ PB and AQ ⊥ QB
Therefore, BP and BQ are the tangents to the circle with centre A.
Similarly, AR and AS are the tangents to the circle with centre B.
6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution – Steps of construction:
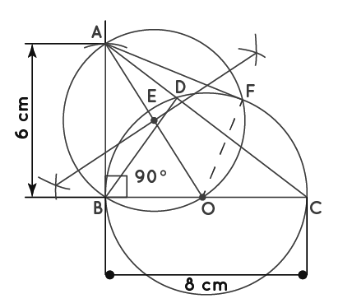
Step I – Draw BC = 8 cm
Step II – Draw the perpendicular at B and cut BA = 6 cm on it. Join AC and right ΔABC is obtained.
Step III – Draw BD perpendicular to AC.
Step IV – Since ∠BDC = 90° and the circle has to pass through B, C and D, BC must be the diameter of this circle. So, take O as the midpoint of BC and with O as centre and OB as radius draw a circle that will pass through B, C and D.
Step V – To draw tangents from A to the circle with centre O.
Step VI – Join OA, and draw its perpendicular bisector to intersect OA at point E.
Step VII – With E as centre and EA as radius draw a circle that intersects the previous circle at B and F.
Step VIII – Join AF.
Step IX – Thus, AF and AB are the required tangents to the circle with centre O.
Proof:
∠ABO = ∠AFO = 90° (Angle in a semi-circle)
∴ AB ⊥ OB and AF ⊥ OF (We know that the line joining the centre of a circle to the tangent is always perpendicular)
Hence AB and AF are the tangents from A to the circle with centre O.
7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution – Steps of construction:
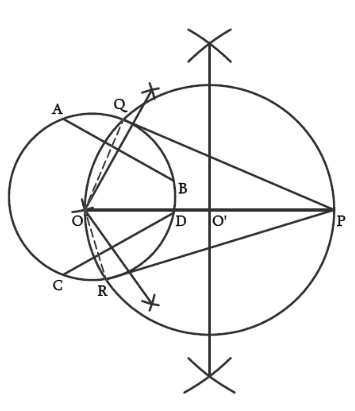
Step I – Draw any circle using a bangle.
Step II – To find its centre:
- Draw two chords on the circle say AB and CD.
- Draw the perpendicular bisectors of AB and CD to intersect at O.
Step III – Now, ‘O’ is the centre of the circle (since the perpendiculars drawn from the centre of a circle to any chord bisect the chord and vice versa).
Step IV – To draw the tangents from a point ‘P’ outside the circle:
- Take a point P outside the circle and draw the perpendicular bisector of OP which meets at OP at O’.
- With O’ as the centre and OO’ as radius draw a circle that cuts the given circle at Q and R.
- Join PQ and PR.
Step V – Thus, PQ and PR are the required tangents.
Proof
∠QOP = ∠ORP = 90° (Angle in a semi-circle)
∴ OQ ⊥ QP and OR ⊥ RP. (We know that the line joining the centre of a circle to the tangent is always perpendicular)
Hence, we have PQ and PR as the tangents to the given circle.
Go Back To Chapters

Leave a Reply