NCERT Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.4

NCERT Solutions Class 10 Maths
Chapter – 2 (Polynomials)

The NCERT Solutions in English Language for Class 10 Mathematics Chapter – 2 Polynomials Exercise 2.4 has been provided here to help the students in solving the questions from this exercise.

Chapter : 2 Polynomials

Exercise – 2.4

1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x³+ x²– 5x + 2; $\boldsymbol{-\frac{1}{2}}$ , 1, -2
(ii) x³– 4x²+ 5x – 2; 2, 1, 1

Solution –
(i) 2x³+ x²– 5x + 2; $\boldsymbol{\frac{1}{2}}$ , 1, -2
p(x) = 2x³+ x²– 5x + 2
Given zeroes are $\frac{1}{2}$ , 1, – 2
Substitute x = $\frac{1}{2}$ in p (x) = 2x³ + x² – 5x + 2
∴ p(1/2) = 2(1/2)³+ (1/2)²– 5(1/2) + 2
= (1/4) + (1/4) – (5/2) + 2
= 0
Substitute x = 1 in p (x) = 2x³ + x² – 5x + 2
p(1) = 2(1)³+ (1)²– 5(1) + 2
= 2 + 1 – 5 + 2
= 0
Substitute x = -2 in p (x) = 2x³ + x² – 5x + 2
p(-2) = 2(-2)³+ (-2)²– 5(-2) + 2
= 2 × (-8) + 4 + 10 +2
= -16 + 16
= 0
Hence, proved 1/2, 1, -2 are the zeroes of 2x³+x²-5x+2.
Now, comparing the given polynomial with general expression, we get;
∴ ax³+ bx²+ cx + d = 2x³+ x²– 5x + 2
a = 2, b = 1, c = -5 and d = 2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax³+ bx²+ cx + d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α βγ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α + β + γ
= ½ + 1 + (-2)
= -½ = –b/a
αβ + βγ + γα
= (½ × 1) + (1 × -2) + (-2 × ½)
= -5/2
= c/a
α β γ
= ½ × 1 × (-2)
= -2/2
= -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.

(ii) x³– 4x²+ 5x – 2; 2, 1, 1
Given, p(x) = x³– 4x²+ 5x – 2
Given zeroes are 2, 1, 1
Substitute x = 2 in p (x) = x³ – 4x² + 5x – 2
p (2) = (2)³ – 4(2)² + 5(2) – 2
p (2) = 8 – 16 + 10 – 2
p (2) = 18 – 18
p (2) = 0

Substitute x = 1 in x³ – 4x² + 5x – 2
p (1) = (1)³ – 4(1)² + 5(1) – 2
p (1) = 1 – 4 + 5 – 2
p (1) = – 3 + 3
p (1) = 0
Therefore, 2,1 and 1 are the zeroes of the polynomial.
∴ ax³+ bx²+ cx + d = x³– 4x²+5x – 2
a = 1, b = -4, c = 5 and d = -2
Now let α = 2, β = 1 and γ = 1
As we know, if α, β, γ are the zeroes of the cubic polynomial ax³+ bx²+ cx + d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α β γ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α + β + γ
= 2 + 1 + 1
= 4
= -(-4)/1 = –b/a
αβ + βγ + γα
= 2 × 1 + 1 × 1 + 1 × 2
= 5
= 5/1 = c/a
αβγ
= 2 × 1 × 1
= 2
= -(-2)/1 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.

2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Solution –
Let the polynomial be ax³+ bx²+ cx + d and the zeroes be α, β and γ.
As per the given question,
α + β + γ
= -b/a
= 2/1
αβ + βγ + γα
= c/a
= -7/1
αβγ
= -d/a
= -14/1
Thus, from above three expressions we get the values of coefficient of polynomial.
a = 1, b = -2, c = -7, d = 14
Now, substitute the values of a, b, c, and d in the cubic polynomial ax³ + bx² + cx + d.
Hence, the cubic polynomial is x³– 2x²– 7x + 14

3. If the zeroes of the polynomial x³-3x²+x+1 are a – b, a, a + b, find a and b.

Solution –
We are given with the polynomial here,
p(x) = x³– 3x²+ x + 1
zeroes are given as a – b, a, a + b
Now, comparing the given polynomial with general expression, we get;
∴ px³+ qx²+ rx + s
= x³– 3x²+ x + 1
p = 1, q = -3, r = 1 and s = 1
Sum of zeroes = -q/p
= a – b + a + a + b
= 3a
Putting the values q and p.
-q/p = -(-3)/1
3a = 3
a = 1
Thus, the zeroes are 1 – b, 1, 1 + b.
Now, product of zeroes = 1(1 – b)(1 + b)
-s/p = 1 – b²

-1/1 = 1 – b²

-1 = 1 – b²
b²= 1 + 1 = 2
b = ±√2
Hence,1 – √2, 1 ,1 + √2 are the zeroes of x³– 3x²+ x + 1.

4. If two zeroes of the polynomial x⁴– 6x³– 26x²+ 138x – 35 are 2 ± √3, find other zeroes.

Solution –
Given polynomial is x⁴ – 6x³ – 26x² + 138x – 35 and the zeroes of the polynomial are 2 ± √3
Since this is a polynomial equation of degree 4, hence there will be total 4 roots.
Let f(x) = x⁴– 6x³– 26x²+ 138x – 35
Since 2 + √3 and 2 – √3 are zeroes of given polynomial f(x).
∴ [x − (2 + √3)] [x − (2 – √3)] = 0
(x − 2 − √3)(x − 2 + √3) = 0
x²– 4x + 1, this is a factor of a given polynomial f(x).
Now, if we will divide f(x) by g(x), the quotient will also be a factor of f(x) and the remainder will be 0.
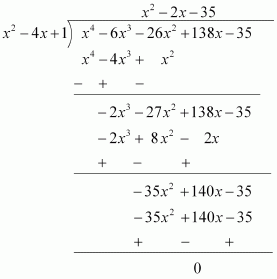
NCERT Class 10 Maths Solution
So, x⁴– 6x³– 26x²+ 138x – 35 = (x²– 4x + 1)(x² – 2x − 35)
Now, on further factorizing (x²– 2x − 35) we get,
x²– (7 − 5)x − 35
⇒ x²– 7x + 5x + 35 = 0
⇒ x(x −7)+5(x−7) = 0
⇒ (x+5)(x−7) = 0
So, its zeroes are given by:
x= −5 and x = 7.
Therefore, all four zeroes of given polynomial equation are: 2 + √3 , 2 – √3, −5 and 7.

5. If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.

Solution –
By division algorithm,
Dividend = Divisor × Quotient + Remainder
Dividend − Remainder = Divisor × Quotient
Let’s divide x⁴ – 6x³ + 16x² – 25x + 10 by x² – 2x + k.
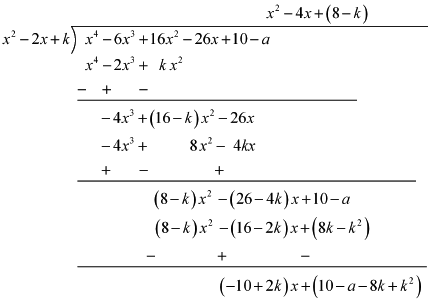
NCERT Class 10 Maths Solution
It can be observed that (-10 + 2k)x + (10 – a – 8k + k²) will be 0.
Therefore, (-10 + 2k) = 0 and (10 – a – 8k + k²) = 0
For (-10 + 2k) = 0,
2k = 10
k = 5

For (10 – a – 8k + k²) = 0
10 − a − 8 × 5 + 25 = 0
10 − a − 40 + 25 = 0
− 5 − a = 0
a = −5
Therefore, k = 5 and a = -5.

Go Back To Chapters

NCERT Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.4